Question

【题目】(1)已知f(x)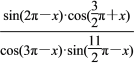＝，求f(－)的值

(2)已知－π<x<0，sin(π＋x)－cosx＝－.

①求sinx－cosx的值；②求的值.

Answer 1

【答案】（1）－1.（2）①－.②－.

【解析】试题分析：（1）解析式利用诱导公式化简，再利用同角三角函数间基本关系变形，将 代入计算即可求出值；（2）①利用 ，将 和 平方，即可求出结果，注意 与 的大小关系；②利用二倍角公式和同角三角函数的基本关系，代入相应的值即可求出结果.

.

试题解析：(1)f(x)＝＝－tan2x，

f(－)＝－tan2(－)＝－tan2π＝－1.

解　①由已知，得sinx＋cosx＝， sin2x＋2sinxcosx＋cos2x＝，

整理得2sinxcosx＝－.∵(sinx－cosx)2＝1－2sinxcosx＝.

由－π<x<0，知sinx<0， 又sinx＋cosx>0，∴cosx>0，sinx－cosx<0，

故sinx－cosx＝－.

②＝＝＝＝－.