题目内容
【题目】在四棱锥P—ABCD中,![]() PAB为正三角形,四边形ABCD为炬形,平面PAB⊥平面ABCD.AB=2AD,M,N分别为PB,PC中点.
PAB为正三角形,四边形ABCD为炬形,平面PAB⊥平面ABCD.AB=2AD,M,N分别为PB,PC中点.

(1)求证:MN//平面PAD;
(2)求二面角B—AM—C的大小;
(3)在BC上是否存在点E,使得EN⊥平面AMV?若存在,求![]() 的值:若不存在,请说明理由.
的值:若不存在,请说明理由.
【答案】(1)证明见解析(2)45°(3)存在,![]()
【解析】
(1)欲证![]() //平面
//平面![]() ,则证明MN∥AD即可.
,则证明MN∥AD即可.
(2)取![]() 中点
中点![]() 再建立空间直角坐标系,求得
再建立空间直角坐标系,求得![]() 与
与![]() 的法向量再求解即可.
的法向量再求解即可.
(3)设![]() 再根据
再根据![]() 平面
平面![]() ,列出对应的向量,利用数量积为0,求出
,列出对应的向量,利用数量积为0,求出![]() 再计算即可.
再计算即可.
证明:(1)∵M,N分别是PB,PC中点
∴MN是△ABC的中位线
∴MN∥BC∥AD
又∵AD![]() 平面PAD,MN
平面PAD,MN![]() 平面PAD
平面PAD
所以MN∥平面PAD.
解:(2)过点P作PO垂直于AB,交AB于点O,
因为平面PAB⊥平面ABCD,所以PO⊥平面ABCD,
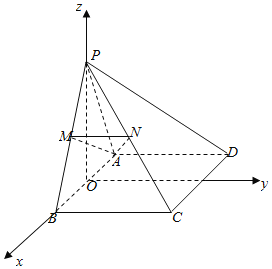
如图建立空间直角坐标系,
设AB=2,则A(﹣1,0,0),C(1,1,0),
M(![]() ,0,
,0,![]() ),
),
B(1,0,0),N(![]() ),
),
则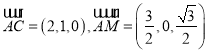
设平面CAM法向量为![]() ,
,
由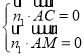 ,得
,得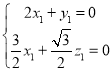 ,
,
令x1=1,则![]() ,即
,即![]()
平面ABM法向量![]()
所以,二面角B﹣AM﹣C的余弦值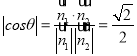
因为二面角B﹣AM﹣C是锐二面角,
所以二面角B﹣AM﹣C等于45°
(3)存在点E,使得EN⊥平面AMN
设E(1,λ,0),则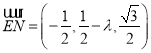 ,
,
由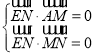 可得
可得![]() ,
,
所以在BC存在点E,使得EN⊥平面AMN,
此时![]() .
.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目