Question

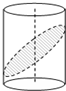如图，平面截圆柱，截面是一个椭圆，若截面与圆柱底面所成的角为60°，则椭圆的离心率为（　　）

• A．

  15

  15

• B．

  33

  6

• C．

  3

  2

• D．

  5

  3

Answer 1

分析：本题根据椭圆的几何特征来求解，椭圆上两点间的最长距离是长轴长，最短距离是短轴长，由本题条件可以得出短轴长即圆柱的直径，而长轴长可以在轴截面中求解．

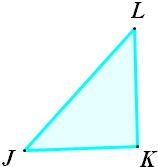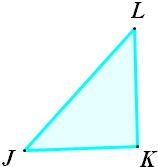解答：解：设圆柱的底面直径为2a，所以由意可得椭圆的短轴长是2a，
因为面与圆柱底面所成的角为60°，
所以过椭圆长轴的轴截面图形如图，
∠KJL=60°，JK是底面直径长度为2a，
由此三角形是直角三角形，可得LJ=4a，
∴椭圆的长轴长为4a，短轴长为2a，
所以椭圆的焦距为2

3

a，
所以椭圆的离心率为e=

3

2

．

点评：本题考查与二面角有关的立体几何综合题，以及椭圆的性质，是解析几何与立体几何结合的一道综合题．