题目内容
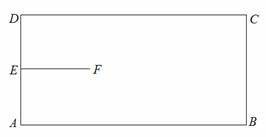
如图,矩形ABCD是机器人踢足球的场地,AB=170cm,AD=80cm,机器人先从AD的中点E进入场地到点F处,EF=40cm,EF⊥AD.场地内有一小球从B点向A点运动,机器人从F点出发去截小球,现机器人和小球同时出发,它们均作匀速直线运动,并且小球运动的速度是机器人行走速度的2倍.若忽略机器人原地旋转所需的时间,则机器人最快可在何处截住小球?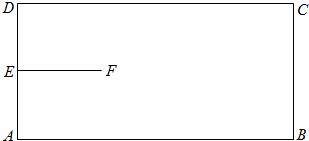
分析:设机器人最快可在点G处截住小球,点G在线段AB上,设FG为xcm,表示出BG和AG因为三角形AEF为等腰直角三角形,可得角FAG为45°,在三角形AFG中根据余弦定理求出FG即可.
解答:解:设该机器人最快可在点G处截住小球,点G在线段AB上.
设FG=xcm.根据题意,得BG=2xcm.
则AG=AB-BG=(170-2x)(cm).
连接AF,在△AEF中,EF=AE=40cm,EF⊥AD,
所以∠EAF=45°,AF=40
cm.
于是∠FAG=45°.在△AFG中,由余弦定理,
得FG2=AF2+AG2-2AF•AGcos∠FAG.
所以x2=(40
)2+(170-2x)2-2×40
×(170-2x)cos45°.
解得x1=50x2=
.
所以AG=170-2x=70(cm),或AG=-
(cm)(不合题意,舍去).
答:该机器人最快可在线段AB上离A点70cm处截住小球.
设FG=xcm.根据题意,得BG=2xcm.
则AG=AB-BG=(170-2x)(cm).
连接AF,在△AEF中,EF=AE=40cm,EF⊥AD,
所以∠EAF=45°,AF=40
| 2 |
于是∠FAG=45°.在△AFG中,由余弦定理,
得FG2=AF2+AG2-2AF•AGcos∠FAG.
所以x2=(40
| 2 |
| 2 |
解得x1=50x2=
| 370 |
| 3 |
所以AG=170-2x=70(cm),或AG=-
| 230 |
| 3 |
答:该机器人最快可在线段AB上离A点70cm处截住小球.
点评:考查学生根据实际问题选择函数类型的能力,利用余弦定理求边的能力.

练习册系列答案
相关题目