Question

（本题满分14分）

       如图，矩形ABCD是机器人踢球的场地，AB=170cm，AD=80cm，机器人先从AD中点E进入场地到点F处，EF=40cm，EF⊥AD。场地内有一小球从B点向A点运动，机器人从F点出发去截小球。现机器人和小球同时出发，它们均作直线运动，并且小球运动的速度是机器人行走速度的2倍。若忽略机器人圆底旋转所需的时间，则机器人最快可在何处截住小球？

Answer 1

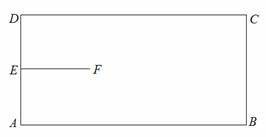
（本题满分14分）

解：设该机器人最快可在G点处截住小球 ，点G在线段AB上．

设．根据题意，得．

则．………………………………………………1分

连接AF，在△AEF中，EF=AE=40cm，EF⊥AD，

所以， ．………………………………………………2分

于是．在△中，由余弦定理，

得．

所以．………………8分

解得．………………………………………………………………12分

所以，

或（不合题意，舍去）．………13分

答：该机器人最快可在线段AB上离A点70cm处截住小球．……………………14分

       解法二：设该机器人最快可在G处截住小球，点G在线段AB上。

       设cm，根据题意，得cm

       过F作FH⊥AB，垂足为H。

       ∵AE=EF=40cm，EF⊥AD，∠A=90°，

       所以四边形AHFE是正方形。

       则FH=40cm，GH=AB-AH-BG=（130-2x）（cm）……………………2分

       在Rt△FHG中，由勾股定理，得.

       所以……………………………………………………8分

       解得

………………………………………………………………12分

所以，

或（不合题意，舍去）．………13分

答：该机器人最快可在线段AB上离A点70cm处截住小球．……………………14分