题目内容
已知点A(3,1)是直线l被双曲线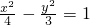 所截得的弦的中点,则直线l的方程是
所截得的弦的中点,则直线l的方程是
- A.9x-4y-23=0
- B.9x+4y-31=0
- C.x-4y+1=0
- D.x+4y-7=0
A
分析:由题意知该直线必存在斜率,设该弦两端点为P(x1,y1),Q(x2,y2),利用平方差法即可求得该直线方程.
解答:由题意知该直线必存在斜率,设该弦两端点为P(x1,y1),Q(x2,y2),
则x1+x2=6,y1+y2=2,
把P,Q两点坐标代入双曲线方程,得 ①,
①, ②,
②,
①-②得, =0,即
=0,即 =0,
=0,
整理得, =
= ×
× =
= ×
×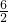 =
= ,即kPQ=
,即kPQ= ,
,
故所求直线方程为:y-1= ,即9x-4y-23=0.
,即9x-4y-23=0.
故选A.
点评:本题考查直线与圆锥曲线的位置关系问题,属中档题,涉及弦中点问题,一般利用平方差法,即设出弦端点,把坐标代入曲线方程,变形为关于中点及直线斜率的关系式.
分析:由题意知该直线必存在斜率,设该弦两端点为P(x1,y1),Q(x2,y2),利用平方差法即可求得该直线方程.
解答:由题意知该直线必存在斜率,设该弦两端点为P(x1,y1),Q(x2,y2),
则x1+x2=6,y1+y2=2,
把P,Q两点坐标代入双曲线方程,得
 ①,
①, ②,
②,①-②得,
 =0,即
=0,即 =0,
=0,整理得,
 =
= ×
× =
= ×
×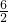 =
= ,即kPQ=
,即kPQ= ,
,故所求直线方程为:y-1=
 ,即9x-4y-23=0.
,即9x-4y-23=0.故选A.
点评:本题考查直线与圆锥曲线的位置关系问题,属中档题,涉及弦中点问题,一般利用平方差法,即设出弦端点,把坐标代入曲线方程,变形为关于中点及直线斜率的关系式.

练习册系列答案
相关题目
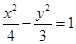 所截得的弦的中点,则直线l的方程是( )
所截得的弦的中点,则直线l的方程是( )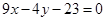 B.
B. C.
C.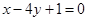 D.
D.
 所截得的弦的中点,则直线l的方程是( )
所截得的弦的中点,则直线l的方程是( ) 外一点,过A倾斜角为
外一点,过A倾斜角为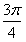 的直线L与椭圆相交于B点和C点。
的直线L与椭圆相交于B点和C点。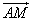 =t。(t为参数)写出L的参数方程;
=t。(t为参数)写出L的参数方程;