题目内容
已知点A(3,1)是直线l被双曲线
-
=1所截得的弦的中点,则直线l的方程是( )
| x2 |
| 4 |
| y2 |
| 3 |
分析:由题意知该直线必存在斜率,设该弦两端点为P(x1,y1),Q(x2,y2),利用平方差法即可求得该直线方程.
解答:解:由题意知该直线必存在斜率,设该弦两端点为P(x1,y1),Q(x2,y2),
则x1+x2=6,y1+y2=2,
把P,Q两点坐标代入双曲线方程,得
-
=1①,
-
=1②,
①-②得,
-
=0,即
-
=0,
整理得,
=
×
=
×
=
,即kPQ=
,
故所求直线方程为:y-1=
(x-3),即9x-4y-23=0.
故选A.
则x1+x2=6,y1+y2=2,
把P,Q两点坐标代入双曲线方程,得
| x12 |
| 4 |
| y12 |
| 3 |
| x22 |
| 4 |
| y22 |
| 3 |
①-②得,
| x12-x22 |
| 4 |
| y12-y22 |
| 3 |
| (x1+x2)(x1-x2) |
| 4 |
| (y1+y2)(y1-y2) |
| 3 |
整理得,
| y1-y2 |
| x1-x2 |
| 3 |
| 4 |
| x1+x2 |
| y1+y2 |
| 3 |
| 4 |
| 6 |
| 2 |
| 9 |
| 4 |
| 9 |
| 4 |
故所求直线方程为:y-1=
| 9 |
| 4 |
故选A.
点评:本题考查直线与圆锥曲线的位置关系问题,属中档题,涉及弦中点问题,一般利用平方差法,即设出弦端点,把坐标代入曲线方程,变形为关于中点及直线斜率的关系式.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
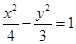 所截得的弦的中点,则直线l的方程是( )
所截得的弦的中点,则直线l的方程是( )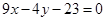 B.
B. C.
C.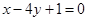 D.
D.
 所截得的弦的中点,则直线l的方程是( )
所截得的弦的中点,则直线l的方程是( ) 外一点,过A倾斜角为
外一点,过A倾斜角为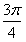 的直线L与椭圆相交于B点和C点。
的直线L与椭圆相交于B点和C点。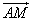 =t。(t为参数)写出L的参数方程;
=t。(t为参数)写出L的参数方程;