题目内容
与椭圆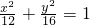 共焦点,离心率互为倒数的双曲线方程是
共焦点,离心率互为倒数的双曲线方程是
- A.

- B.
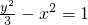
- C.

- D.

A
分析:确定椭圆的焦点坐标与离心率,可得双曲线焦点坐标与离心率,从而可求双曲线的方程.
解答:椭圆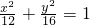 中a2=16,b2=12,c2=4
中a2=16,b2=12,c2=4
∴椭圆的焦点坐标为(0,2),(0,-2),离心率e= =
=
∴双曲线的焦点坐标为(0,2),(0,-2),离心率e′=2
∴c′=2,a′=1,
∴b′2=3
∴与椭圆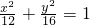 共焦点,离心率互为倒数的双曲线方程是
共焦点,离心率互为倒数的双曲线方程是
故选A.
点评:本题考查椭圆与双曲线的几何性质,考查椭圆与双曲线的标准方程,属于中档题.
分析:确定椭圆的焦点坐标与离心率,可得双曲线焦点坐标与离心率,从而可求双曲线的方程.
解答:椭圆
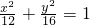 中a2=16,b2=12,c2=4
中a2=16,b2=12,c2=4∴椭圆的焦点坐标为(0,2),(0,-2),离心率e=
 =
=
∴双曲线的焦点坐标为(0,2),(0,-2),离心率e′=2
∴c′=2,a′=1,
∴b′2=3
∴与椭圆
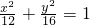 共焦点,离心率互为倒数的双曲线方程是
共焦点,离心率互为倒数的双曲线方程是
故选A.
点评:本题考查椭圆与双曲线的几何性质,考查椭圆与双曲线的标准方程,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 共焦点,它们的离心率之和为
共焦点,它们的离心率之和为 ,则双曲线的方程应是
,则双曲线的方程应是
 共焦点,它们的离心率之和为
共焦点,它们的离心率之和为 ,则双曲线方程为_____
,则双曲线方程为_____ 共焦点,离心率互为倒数的双曲线方程是( )
共焦点,离心率互为倒数的双曲线方程是( )


