题目内容
已知曲线C：xy=1，过C上一点An（xn，yn）作一斜率为
的直线交曲线C于另一点An+1（xn+1，yn+1），点列An（n=1，2，3，…）的横坐标构成数列{xn}，其中
．
（1）求xn与xn+1的关系式；
（2）求证：{
}是等比数列；
（3）求证：（﹣1）
+（﹣1）2x2+（﹣1）3x3+…+（﹣1）nxn＜1（n∈N，n≥1）．
的直线交曲线C于另一点An+1（xn+1，yn+1），点列An（n=1，2，3，…）的横坐标构成数列{xn}，其中．（1）求xn与xn+1的关系式；
（2）求证：{
}是等比数列；（3）求证：（﹣1）
+（﹣1）2x2+（﹣1）3x3+…+（﹣1）nxn＜1（n∈N，n≥1）．解：（1）过C：
上一点An（xn，yn）作斜率为kn的直线交C于另一点An+1，
则
，
于是有：xnxn+1=xn+2
即：
．
（2）记
，
则
，
因为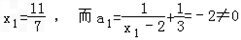
，
因此数列{
}是等比数列．
（3）由（2）知：
，
．
①当n为偶数时有：（﹣1）n﹣1 xn﹣1+（﹣1）nxn=
，
于是在n为偶数时有：
．
②在n为奇数时，前n﹣1项为偶数项，
于是有：（﹣1）
+（﹣1）2x2++（﹣1）n﹣1xn﹣1+（﹣1）nxn
．
综合①②可知原不等式得证．
上一点An（xn，yn）作斜率为kn的直线交C于另一点An+1，则
，于是有：xnxn+1=xn+2
即：
．（2）记
，则
，因为
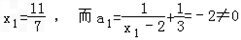，因此数列{
}是等比数列．（3）由（2）知：
，．①当n为偶数时有：（﹣1）n﹣1 xn﹣1+（﹣1）nxn=
，于是在n为偶数时有：
．②在n为奇数时，前n﹣1项为偶数项，
于是有：（﹣1）
+（﹣1）2x2++（﹣1）n﹣1xn﹣1+（﹣1）nxn．综合①②可知原不等式得证．
练习册系列答案
相关题目