题目内容
已知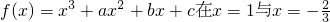 时都取得极值.
时都取得极值.
(Ⅰ)求a,b的值;
(Ⅱ)若x∈[-1,2],都有f(x)-c2<0成立,求c的取值范围.
解:(Ⅰ)由已知,f'(x)=3x2+2ax+b,∵ 时取极值,
时取极值,
∴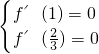 即
即
解得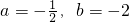 ,故a,b的值为:
,故a,b的值为: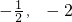
(Ⅱ)(解法一)由(I)知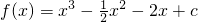 .由
.由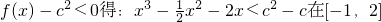 上恒成立.
上恒成立.
设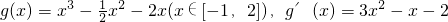 .…(8分)
.…(8分)
由 .…(10分)
.…(10分)
∴[g(x)]max=2,∴2<c2-c解得,c<-1或c>2.,
∴c的取值范围为(-∞,-1)∪(2,+∞).
(解法二)由(I)知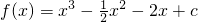 .,∴f'(x)=3x2-x-2.…(8分)
.,∴f'(x)=3x2-x-2.…(8分)
①当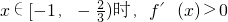 ;②当
;②当 ;
;
③当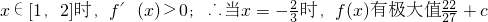 .
.
而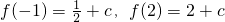 ,…(10分)
,…(10分)
∴当x∈[1,2]时,f(x)的最大值为f(2)=2+c.
对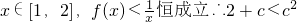 ,
,
故c的取值范围为(-∞,-1)∪(2,+∞).…(12分)
分析:(Ⅰ)由极值的定义可知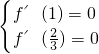 解此方程组可得a、b的值;
解此方程组可得a、b的值;
(Ⅱ)解法一通过分离常数把问题转化为求函数g(x)=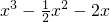 在区间[-1,2]上的最大值问题;解法二则把问题恒成立转化为求函数f(x)在区间[-1,2]上的最大值问题.
在区间[-1,2]上的最大值问题;解法二则把问题恒成立转化为求函数f(x)在区间[-1,2]上的最大值问题.
点评:本题考查函数的极值与最值,通过求解函数的最值来解决恒成立问题是解决问题的关键,属中档题.
 时取极值,
时取极值,∴
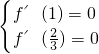 即
即
解得
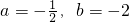 ,故a,b的值为:
,故a,b的值为: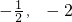
(Ⅱ)(解法一)由(I)知
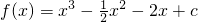 .由
.由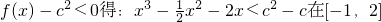 上恒成立.
上恒成立.设
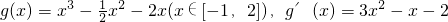 .…(8分)
.…(8分)由
 .…(10分)
.…(10分)∴[g(x)]max=2,∴2<c2-c解得,c<-1或c>2.,
∴c的取值范围为(-∞,-1)∪(2,+∞).
(解法二)由(I)知
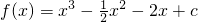 .,∴f'(x)=3x2-x-2.…(8分)
.,∴f'(x)=3x2-x-2.…(8分)①当
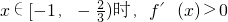 ;②当
;②当 ;
;③当
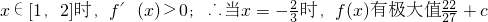 .
.而
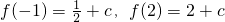 ,…(10分)
,…(10分)∴当x∈[1,2]时,f(x)的最大值为f(2)=2+c.
对
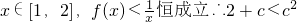 ,
,故c的取值范围为(-∞,-1)∪(2,+∞).…(12分)
分析:(Ⅰ)由极值的定义可知
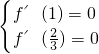 解此方程组可得a、b的值;
解此方程组可得a、b的值;(Ⅱ)解法一通过分离常数把问题转化为求函数g(x)=
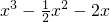 在区间[-1,2]上的最大值问题;解法二则把问题恒成立转化为求函数f(x)在区间[-1,2]上的最大值问题.
在区间[-1,2]上的最大值问题;解法二则把问题恒成立转化为求函数f(x)在区间[-1,2]上的最大值问题.点评:本题考查函数的极值与最值,通过求解函数的最值来解决恒成立问题是解决问题的关键,属中档题.

练习册系列答案
相关题目