题目内容
已知
(1)求 的极值,
的极值,
并证明:若 有
有 ;
;
(2)设 ,且
,且 ,
, ,
,
证明: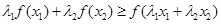 ,
,
若 ,由上述结论猜想一个一般性结论(不需要证明);
,由上述结论猜想一个一般性结论(不需要证明);
(3)证明:若 ,则
,则
【答案】
(1)0,利用作差法即可证明;(2)利用综合法即可证明,猜想:若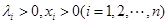 ,且
,且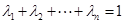 时有
时有
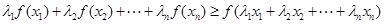 ;(3)利用第(2)问的结论及对数的运算证明即可
;(3)利用第(2)问的结论及对数的运算证明即可
【解析】
试题分析:(1)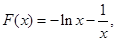 则
则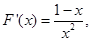
当x∈(0,1)时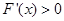 ,x∈(1,+∞)时
,x∈(1,+∞)时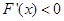 ,
,
∴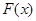 在(0,1)递增,在(1,+∞)递减,
在(0,1)递增,在(1,+∞)递减,
,∴当x=1时,F(x)有极大值为0,且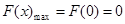 2分
2分
∴当 时
时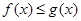 恒成立,即
恒成立,即 时
时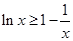 恒成立。
恒成立。
∴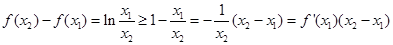 4分
4分
(2)证明:设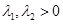 ,且
,且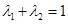 ,令
,令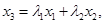 ,则
,则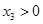 ,且
,且
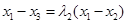 ,
,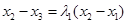 ,
,
由(1)可知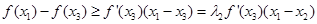 ①
①
 ②
②
①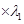 +②
+②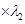 ,得
,得
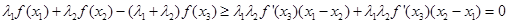
∴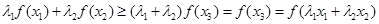 8分
8分
猜想:若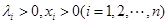 ,且
,且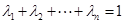 时有
时有
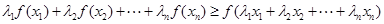 9分
9分
(3)证明:令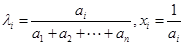
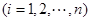
由猜想结论得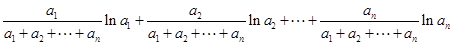
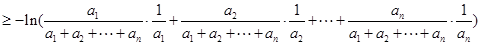
=
∴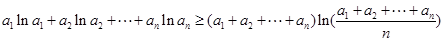 ,
,
即有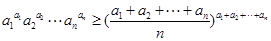 。 14分
。 14分
考点:本题考查了导数的运用
点评:导数本身是个解决问题的工具,是高考必考内容之一,高考往往结合函数甚至是实际问题考查导数的应用,求单调、最值、完成证明等,请注意归纳常规方法和常见注意点

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
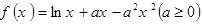 .
.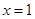 是函数
是函数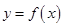 的极值点,求
的极值点,求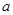 的值;
的值;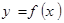 的单调区间.
的单调区间.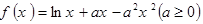 .
.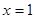 是函数
是函数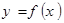 的极值点,求
的极值点,求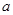 的值;
的值; .
. 的极值,并证明:若
的极值,并证明:若 有
有 ;
;
 ,且
,且 ,
, ,证明:
,证明: ,
, ,由上述结论猜想一个一般性结论(不需要证明);
,由上述结论猜想一个一般性结论(不需要证明); ,则
,则 .
.