题目内容
已知x、y满足约束条件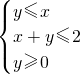 ,若点P的坐标为(
,若点P的坐标为( ,-2),点Q为该区域内一点,则|PQ|长的最小值是 ________.
,-2),点Q为该区域内一点,则|PQ|长的最小值是 ________.
2
分析:先画出满足条件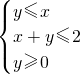 的平面区域,再把|PQ|的最小值转化为点可行域内的Q到P(
的平面区域,再把|PQ|的最小值转化为点可行域内的Q到P( ,-2)的距离的最小值即可.
,-2)的距离的最小值即可.
解答: 解:由题可知不等式组确定的区域为阴影部分包括边界,
解:由题可知不等式组确定的区域为阴影部分包括边界,
可行域内的Q到P( ,-2)的距离的最小值,由图可知
,-2)的距离的最小值,由图可知
|PQ|min等于点P到x轴的距离,即为:2,
故答案为:2.
点评:本题属于线性规划中的延伸题,对于可行域不要求线性目标函数的最值,而是求可行域内的点与P之间的距离问题
分析:先画出满足条件
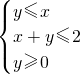 的平面区域,再把|PQ|的最小值转化为点可行域内的Q到P(
的平面区域,再把|PQ|的最小值转化为点可行域内的Q到P( ,-2)的距离的最小值即可.
,-2)的距离的最小值即可.解答:
 解:由题可知不等式组确定的区域为阴影部分包括边界,
解:由题可知不等式组确定的区域为阴影部分包括边界,可行域内的Q到P(
 ,-2)的距离的最小值,由图可知
,-2)的距离的最小值,由图可知|PQ|min等于点P到x轴的距离,即为:2,
故答案为:2.
点评:本题属于线性规划中的延伸题,对于可行域不要求线性目标函数的最值,而是求可行域内的点与P之间的距离问题

练习册系列答案
相关题目
 ,且
,且 ,若变量x,y满足约束条
,若变量x,y满足约束条 ,则z的最大值为
,则z的最大值为
 则z=2x-3y的最大值 .
则z=2x-3y的最大值 . 的最小值是
的最小值是