题目内容
若函数f(x)=
(x∈R)的值域为［-1,4］,求实数a、b的值.
令y=
y·x2-ax+y-b=0,
当y≠0时,上式有解,则Δ=a2-4y(y-b)≥0
4y2-4yb-a2≤0.
又y∈［-1,4］,则4y2-4by-a2=0的两根为-1、4.
∴
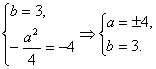
∴a=±4,b=3,y=0时也成立.
∴a=±4,b=3.
练习册系列答案
相关题目
若函数f（x）满足条件：当x1，x2∈[-1，1]时，有|f（x1）-f（x2）|≤3|x1-x2|成立，则称f（x）∈Ω．对于函数g（x）=x3，h（x）=
，有（ ）
| 1 |
| x+2 |
| A、g（x）∈Ω且h（x）∉Ω |
| B、g（x）∉Ω且h（x）∈Ω |
| C、g（x）∈Ω且h（x）∈Ω |
| D、g（x）∉Ω且h（x）∉Ω |
