题目内容
设函数![]() ,其图象在点
,其图象在点![]() ,
,![]() 处的切线的斜率分别为
处的切线的斜率分别为![]()
(I)求证:![]() ;
;
(II)若函数![]() 的递增区间为
的递增区间为![]() ,求|
,求|![]() |的取值范围;
|的取值范围;
(III)若当![]() 时(
时(![]() 是与
是与![]() 无关的常数),恒有
无关的常数),恒有![]() ,试求
,试求![]() 的最小值。
的最小值。
![]() ,
,![]()
解析:
(I)![]() 由题意及导数的几何意义得
由题意及导数的几何意义得
![]() ①
① ![]() ②
②
又![]()
由①得![]() ③
③
将![]() 代入②得
代入②得![]() 有实根,
有实根,
故判别式![]() ④
④
由③、④得![]()
(II)由![]()
知方程![]() (*)有两个不等实根,设为x1,x2,
(*)有两个不等实根,设为x1,x2,
又由![]() (*)的一个实根,
(*)的一个实根,
则由根与系数的关系得![]()
当![]() 或
或![]() 时,
时,![]()
故函数![]() 的递增区间为
的递增区间为![]() ,由题设知
,由题设知![]() ,
,
因此![]() ,故
,故![]()
![]() 的取值范围为
的取值范围为![]()
(Ⅲ)由![]()
![]()
又![]() ,故得
,故得![]()
设![]() 的一次或常数函数,由题意,
的一次或常数函数,由题意,
![]() 恒成立
恒成立
故![]()
由题意![]()

练习册系列答案
相关题目
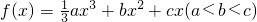 ,其图象在点A(1,f(1)),B(m,f(m))处的切线的斜率分别为0,-a.
,其图象在点A(1,f(1)),B(m,f(m))处的切线的斜率分别为0,-a. ;
; ,其图象在点A(1,f(1)),B(m,f(m))处的切线的斜率分别为0,-a.
,其图象在点A(1,f(1)),B(m,f(m))处的切线的斜率分别为0,-a. ;
;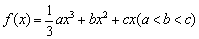 ,其图象在点
,其图象在点 处的切线的斜率分别为
处的切线的斜率分别为 .
.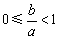 ;
; 的递增区间为
的递增区间为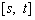 ,求
,求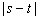 的取值范围.
的取值范围.