题目内容
已知某生产厂家的年利润y(单位:万元)与年产量x(单位:万件)的函数关系式为y=-
x3+81x-234,则使该生产厂家获得最大年利润的年产量为 万件.
| 1 |
| 3 |
考点:函数模型的选择与应用
专题:计算题,函数的性质及应用,导数的综合应用
分析:由题意,求导y′=-x2+81=(9-x)(9+x),从而确定函数的最大值点.
解答:
解:∵y=-
x3+81x-234,
∴y′=-x2+81=(9-x)(9+x),
则y=-
x3+81x-234在(0,9)上单调递增,
在[9,+∞)上单调递减,
故当x=9时,函数有最大值,
故答案为:9.
| 1 |
| 3 |
∴y′=-x2+81=(9-x)(9+x),
则y=-
| 1 |
| 3 |
在[9,+∞)上单调递减,
故当x=9时,函数有最大值,
故答案为:9.
点评:本题考查了函数在实际问题中的应用及导数的综合应用,属于中档题.

练习册系列答案
相关题目
下列说法中,错误的是( )
| A、有时可以把分类变量的不同取值用数字表示,但这时的数字除了分类以外没有其他含义 |
| B、在统计学中,独立性检验就是检验两个分类变量是否有关系的一种方法 |
| C、在进行独立性检验时,可以先利用二维条形图粗略的判断两个分类变量是否有关系 |
| D、通过二维条形图可以精确的给出所得结论的可靠程度 |
a、b是不互相垂直的异面直线,α、β是分别过a、b的平面,则下列四种情况:
①α∥β;②α⊥β;③a∥β;④a⊥β,
其中可能出现的有( )
①α∥β;②α⊥β;③a∥β;④a⊥β,
其中可能出现的有( )
| A、1种 | B、2种 | C、3种 | D、4种 |
已知函数f(x)=x+
-2在区间(2,4)内有唯一零点,则b的取值范围是( )
| b |
| x |
| A、R |
| B、(-∞,0) |
| C、(-8,+∞) |
| D、(-8,0) |
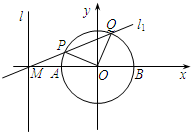 已知直线l的方程为x=-2,且直线l与x轴交于点M,圆O:x2+y2=1与x轴交于A,B两点(如图).
已知直线l的方程为x=-2,且直线l与x轴交于点M,圆O:x2+y2=1与x轴交于A,B两点(如图).