题目内容
(Ⅰ)已知f(x)=x3+x,求这个函数的图象在点x=0处的切线方程;(Ⅱ)计算
 +
+ .
.
【答案】分析:(I)利用导数的几何意义即可得到切线的斜率,进而得到切线的方程;
(II)利用导数的运算法则和微积分基本定理即可得出.
解答:解:(Ⅰ)∵f(x)=x3+x,
∴f'(x)=3x2+1,∴f'(0)=1,
这个函数的图象在点x=0处的切线的斜率为1,
又f(0)=0,∴切点为(0,0)
故切线方程为:y=x.
(Ⅱ)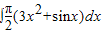 +
+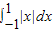 =
=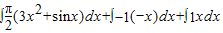 =
=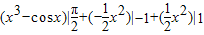 =
=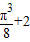 .
.
点评:熟练掌握导数的运算法则和微积分基本定理、导数的几何意义、切线的方程等是解题的关键.
(II)利用导数的运算法则和微积分基本定理即可得出.
解答:解:(Ⅰ)∵f(x)=x3+x,
∴f'(x)=3x2+1,∴f'(0)=1,
这个函数的图象在点x=0处的切线的斜率为1,
又f(0)=0,∴切点为(0,0)
故切线方程为:y=x.
(Ⅱ)
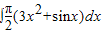 +
+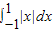 =
=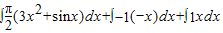 =
=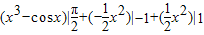 =
=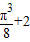 .
.点评:熟练掌握导数的运算法则和微积分基本定理、导数的几何意义、切线的方程等是解题的关键.

练习册系列答案
相关题目