Question

11．如图，在长方体ABCD-A₁B₁C₁D₁中，AB=AD=1，AA₁=2，点P为DD₁的中点．
（1）求异面直线A₁B和AC所成角的余弦值；
（2）求异面直线PC和A₁C₁所成的角．

Answer 1

分析 （1）由AC∥A₁C₁，得∠BA₁C₁是异面直线A₁B和AC所成角，由此利用余弦定理能求出异面直线A₁B和AC所成角的余弦值．
（2）由AC∥A₁C₁，得∠PAC是异面直线PC和A₁C₁所成的角，由此能求出异面直线PC和A₁C₁所成的角．

解答 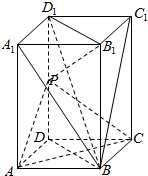解：（1）连结A₁B、A₁C₁、BC₁，
∵在长方体ABCD-A₁B₁C₁D₁中，AB=AD=1，AA₁=2，
∴AC∥A₁C₁，∴∠BA₁C₁是异面直线A₁B和AC所成角，
A₁B=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$，${A}_{1}{C}_{1}=\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$，BC₁=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$，
∴cos∠BA₁C₁=$\frac{{A}_{1}{B}^{2}+{A}_{1}{{C}_{1}}^{2}-B{{C}_{1}}^{2}}{2{A}_{1}B•{A}_{1}{C}_{1}}$=$\frac{5+2-5}{2×\sqrt{5}×\sqrt{2}}$=$\frac{\sqrt{10}}{10}$．
∴异面直线A₁B和AC所成角的余弦值为$\frac{\sqrt{10}}{10}$．
（2）连结AP、AC，
∵AC∥A₁C₁，∴∠PAC是异面直线PC和A₁C₁所成的角，
由已知得AP=PC=AC$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$，
∴∠PAC=60°．
∴异面直线PC和A₁C₁所成的角为60°．

点评 本题考查异面直线所成角的大小的求法，是基础题，解题时要注意余弦定理的合理运用．