题目内容
选修4-5:不等式选讲
设函数f(x)=|2x-1|-|x+1|.
(Ⅰ)求不等式f(x)≤0的解集D;
(Ⅱ)若存在实数x∈D使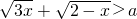 成立,求实数a的取值范围.
成立,求实数a的取值范围.
解:(Ⅰ)当x≤-1时,由f(x)=-x+2≤0,得x≥2,所以x∈∅;
当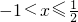 时,由f(x)=-3x≤0得x≥0,所以
时,由f(x)=-3x≤0得x≥0,所以 ;
;
当 时,由f(x)=x-2≤0得x≤2,所以
时,由f(x)=x-2≤0得x≤2,所以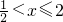 .…(2分)
.…(2分)
综上得:不等式f(x)≤0的解集D={x|0≤x≤2}.…(3分)
(Ⅱ)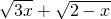 =
=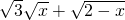 ,…(4分)
,…(4分)
由柯西不等式得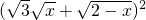 ≤(3+1)(x+(2-x))=8,
≤(3+1)(x+(2-x))=8,
∴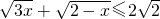 ,…(5分)
,…(5分)
当且仅当 时取“=”,
时取“=”,
∴a的取值范围是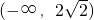 .…(7分)
.…(7分)
分析:(Ⅰ)利用绝对值的几何意义,分类讨论,化简函数,即可求解不等式;
(Ⅱ)利用柯西不等式,确定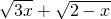 的最小值,即可求得实数a的取值范围.
的最小值,即可求得实数a的取值范围.
点评:本题主要考查绝对值的含义、柯西不等式等基础知识,考查运算求解能力以及推理论证能力,考查函数与方程思想以及分类与整合思想.
当
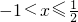 时,由f(x)=-3x≤0得x≥0,所以
时,由f(x)=-3x≤0得x≥0,所以 ;
;当
 时,由f(x)=x-2≤0得x≤2,所以
时,由f(x)=x-2≤0得x≤2,所以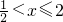 .…(2分)
.…(2分)综上得:不等式f(x)≤0的解集D={x|0≤x≤2}.…(3分)
(Ⅱ)
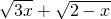 =
=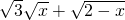 ,…(4分)
,…(4分)由柯西不等式得
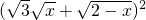 ≤(3+1)(x+(2-x))=8,
≤(3+1)(x+(2-x))=8,∴
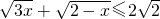 ,…(5分)
,…(5分)当且仅当
 时取“=”,
时取“=”,∴a的取值范围是
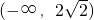 .…(7分)
.…(7分)分析:(Ⅰ)利用绝对值的几何意义,分类讨论,化简函数,即可求解不等式;
(Ⅱ)利用柯西不等式,确定
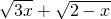 的最小值,即可求得实数a的取值范围.
的最小值,即可求得实数a的取值范围.点评:本题主要考查绝对值的含义、柯西不等式等基础知识,考查运算求解能力以及推理论证能力,考查函数与方程思想以及分类与整合思想.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目