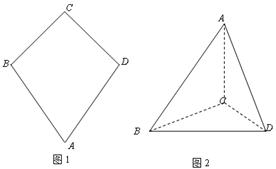
题目内容
如图一,平面四边形![]() 关于直线
关于直线![]() 对称,
对称,![]() .把
.把![]() 沿
沿![]() 折起(如图二),使二面角
折起(如图二),使二面角![]() 的余弦值等于
的余弦值等于![]() .对于图二,完成以下各小题:
.对于图二,完成以下各小题:
(Ⅰ)求![]() 两点间的距离;
两点间的距离;
(Ⅱ)证明:![]() 平面
平面![]() ;
;
(Ⅲ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.

解析:(Ⅰ)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
由![]() ,得:
,得:
![]()
![]() 就是二面角
就是二面角![]() 的平面角,
的平面角,
![]() …………………………2分
…………………………2分
在![]() 中,
中,![]()
![]()
![]()
![]() …………………………4 分
…………………………4 分
(Ⅱ)由![]() ,
,![]()
![]()
![]()
![]()
![]()
![]() …………………………6分
…………………………6分
![]() ,
,
又![]()
![]() 平面
平面![]() . …………………………8分
. …………………………8分
(Ⅲ)方法一:由(Ⅰ)知![]() 平面
平面![]()
![]() 平面
平面![]()
∴平面![]() 平面
平面![]() …………………………10分
…………………………10分
平面![]() 平面
平面![]() ,
,
作![]() 交
交![]() 于
于![]() ,则
,则![]() 平面
平面![]() ,
,
![]() 就是
就是![]() 与平面
与平面![]() 所成的角, …………………………12分
所成的角, …………………………12分
![]() . …………………14分
. …………………14分
方法二:设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
∵![]() …………………10分
…………………10分
![]()
![]() ……………………12分
……………………12分
于是![]() 与平面
与平面![]() 所成角
所成角![]() 的正弦为
的正弦为
![]() . ………………………14分
. ………………………14分
方法三:以![]() 所在直线分别为
所在直线分别为![]() 轴,
轴,![]() 轴和
轴和![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,则
,则

![]() . ………10分
. ………10分
设平面![]() 的法向量为n
的法向量为n![]() ,则
,则
n![]() , n
, n![]() ,
,![]()
![]()
取![]() ,则n
,则n![]() , ----------12分
, ----------12分
于是![]() 与平面
与平面![]() 所成角
所成角![]() 的正弦即
的正弦即
![]() . ……………14分
. ……………14分

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案 关于直线
关于直线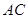 对称,
对称,
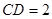 。
。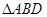 沿
沿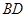 折起(如图二),使二面角
折起(如图二),使二面角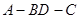 的余弦值等于
的余弦值等于 。对于图二,
。对于图二,
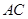 ;
;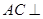 平面
平面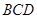 ;
;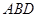 所成角的正弦值。
所成角的正弦值。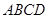 关于直线
关于直线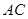 对称,
对称,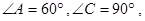
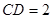 。
。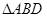 沿
沿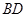 折起(如图二),使二面角
折起(如图二),使二面角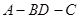 的余弦值等于
的余弦值等于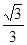 。对于图二,
。对于图二,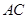 ;(Ⅱ)证明:
;(Ⅱ)证明: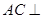 平面
平面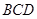 ;
;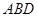 所成角的正弦值。
所成角的正弦值。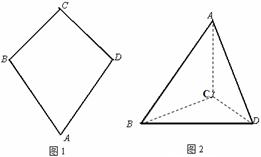
 关于直线
关于直线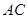 对称,
对称,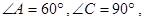
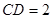 .
.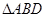 沿
沿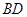 折起(如图二),使二面角
折起(如图二),使二面角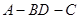 的余弦值等于
的余弦值等于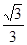 .对于图二,完成以下各小题:
.对于图二,完成以下各小题: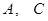 两点间的距离;
两点间的距离;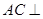 平面
平面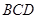 ;
;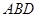 所成角的正弦值.
所成角的正弦值.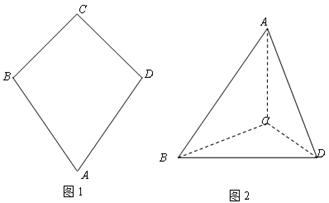
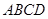 关于直线
关于直线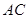 对称,
对称,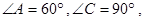
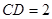 .把
.把 沿
沿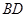 折起(如图二),使二面角
折起(如图二),使二面角 的余弦值等于
的余弦值等于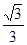 .对于图二,
.对于图二,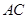 ;
;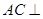 平面
平面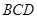 ;
;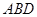 所成角的正弦值.
所成角的正弦值.