题目内容
设关于x的式子
当x∈R时恒有意义，则实数a的取值范围是
- A.a≥0
- B.a＜0
- C.a＜
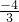
- D.a≥0或a＜
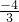
A
分析：由题意得?x∈R，不等式ax2+ax+a+1＞0．当a=0 时，不等式恒成立；当a≠0时，由题意可得△＜0，且a＞0，解得a的范围，将这两种情况下的a的取值范围取并集，即为所求．
解答：由题意得?x∈R，不等式ax2+ax+a+1＞0．
当a=0 时，不等式即1＞0，恒成立．
当a≠0时，由题意可得△=a2-4a（a+1）＜0，且a＞0，
解得a＞0．
综上，实数a的取值范围是[0，+∞），
故选A．
点评：本题考查二次函数的性质，函数的恒成立问题，体现了分类讨论的数学思想，注意检验a=0时的情况，这是解题的易错点．
分析：由题意得?x∈R，不等式ax2+ax+a+1＞0．当a=0 时，不等式恒成立；当a≠0时，由题意可得△＜0，且a＞0，解得a的范围，将这两种情况下的a的取值范围取并集，即为所求．
解答：由题意得?x∈R，不等式ax2+ax+a+1＞0．
当a=0 时，不等式即1＞0，恒成立．
当a≠0时，由题意可得△=a2-4a（a+1）＜0，且a＞0，
解得a＞0．
综上，实数a的取值范围是[0，+∞），
故选A．
点评：本题考查二次函数的性质，函数的恒成立问题，体现了分类讨论的数学思想，注意检验a=0时的情况，这是解题的易错点．
练习册系列答案
相关题目
当x∈R时恒有意义，则实数a的取值范围是（ ）
