题目内容
已知正项等比数列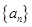 满足:
满足: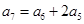 ,若存在两项
,若存在两项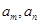 使得
使得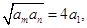 则
则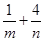 的最小值为( ).
的最小值为( ).
A.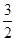 B.
B.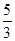 C.
C.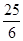 D.不存在
D.不存在
【答案】
A
【解析】
试题分析:因为, ,所以,a5q2=a5q+2a5,q2-q-2=0,解得,q=2。
,所以,a5q2=a5q+2a5,q2-q-2=0,解得,q=2。
又因为,存在两项am,an使得 所以aman=16a12,
所以aman=16a12,
所以,qm+n-2=16, m+n=6。
 =
= (
( )(m+n)
)(m+n)
= (5+
(5+  )≥
)≥ (5+4)=
(5+4)= ,故选A。
,故选A。
考点:本题主要考查等比数列的通项公式,均值定理的应用。
点评:小综合题,通过利用等比数列的知识,得到m+n为定值,从而具备了应用均值定理的两个条件,再通过构造,其第三个条件“三相等”,也具备了。

练习册系列答案
相关题目
 满足:
满足: ,若存在两项
,若存在两项 使得
使得 ,则
,则 的最小值为( )
的最小值为( ) C.
C. D.
D.
 满足:
满足: ,若数列中存在两项
,若数列中存在两项 使得
使得 ,
, 的最小值为( )
的最小值为( )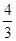 C.
C.
 D.
D. 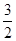
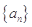 满足:
满足: ,若存在两项
,若存在两项 使得
使得 ,则
,则 的最小值为( )
的最小值为( ) B.
B. C.
C. D.不存在
D.不存在 满足:
满足: ,若存在两项
,若存在两项 使得
使得 ,则
,则 的最小值为( )
的最小值为( )  B.
B. C.
C.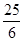 D.不存在
D.不存在 满足
满足 ,若存在两项
,若存在两项 使得
使得 ,则
,则 的最小值是
;
的最小值是
;