题目内容
已知正项等比数列 满足:
满足: ,若存在两项
,若存在两项 使得
使得 ,则
,则 的最小值为( )
的最小值为( )
A. B.
B. C.
C.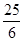 D.不存在
D.不存在
【答案】
A
【解析】
试题分析:根据题意,正项等比数列 满足:
满足: ,故可知
,故可知 ,那么由于存在两项
,那么由于存在两项 使得
使得 ,则可知
,则可知 ,那么可知
,那么可知 ,故选A.
,故选A.
考点:考查了等比数列的性质,以及不等式知识 。
点评:解决该试题的冠军艾女士对于等比中项的理解运用 ,和均值不等式的运用,一正二定三相等,来求最值,属于中档题。

练习册系列答案
相关题目
 满足:
满足: ,若存在两项
,若存在两项 使得
使得 ,则
,则 的最小值为( )
的最小值为( ) C.
C. D.
D.
 满足:
满足: ,若数列中存在两项
,若数列中存在两项 使得
使得 ,
, 的最小值为( )
的最小值为( )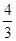 C.
C.
 D.
D. 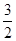
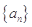 满足:
满足: ,若存在两项
,若存在两项 使得
使得 ,则
,则 的最小值为( )
的最小值为( ) B.
B. C.
C. D.不存在
D.不存在 满足
满足 ,若存在两项
,若存在两项 使得
使得 ,则
,则 的最小值是
;
的最小值是
;