Question

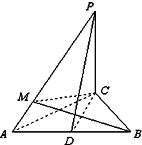
如图，PC⊥平面ABC，PM∥CB，∠ACB=120°，PM=AC=1，BC=2，异面直线AM与直线PC所成的角为60°．
（Ⅰ）求二面角M-AC-B大小的正切值；
（Ⅱ）求三棱锥P-MAC的体积．

Answer 1

分析：（I）在平面ABC内，过C作CD⊥CB，建立空间直角坐标系C-xyz，求出平面MAC的一个法向量为

n

={x1，y1，z1}，平面ABC的法向量取为

m

=（0，0，1）利用 cosθ=

m • n

| m |•| n |

，解答即可．
（II）取平面PCM的法向量取为

n1

=（{1，0，0}），则点A到平面PCM的距离 h=

| CA • n1 |

| n1 |

，求出体积即可．

解答：解：（Ⅰ）在平面ABC内，过点C作CB的垂线，按如图所示建立空间直角坐标系C-xyz．（1分） 
设点P（0，0，z₀）（z₀＞0），由已知可得，点A(

3

2

，-

1

2

，0)，M（0，1，z₀），
则

AM

=(-

3

2

，

3

2

，z0)，

CP

=(0，0，z0)．
因为直线AM与直线PC所成的角为60°，
则

AM

•

CP

=|

AM

|•|

CP

|cos600，即z02=

1

2

z02+3

•z0．
解得z₀=1，从而

CM

=(0，1，1)，

CA

=(

3

2

，-

1

2

，0)．（3分）
设平面MAC的一个法向量为

n

=（x₁，y₁，z₁），
则

n• CM =0 n• CA =0

，即

y1+z1=0 3 2 x1- 1 2 y1=0

．
取x₁=1，则

n

=(1，

3

，-

3

)．（5分）
又

m

=（0，0，1）为平面ABC的一个法向量，
设向量

m

与

n

的夹角为θ，则cosθ=

m•n

|m||n|

=-

3

7

．
从而sinθ=

2

7

，tanθ=-

2 3

3

．（7分）
显然，二面角M-AC-B的平面角为锐角，故二面角M-AC-B的正切值是

2 3

3

．（8分）
（Ⅱ）因为a=（1，0，0）为平面PCM的一个法向量，

CA

=(

3

2

，-

1

2

，0)，
则点A到平面PCM的距离h=

| CA •a|

|a|

=

3

2

．（10分）
又PC=PM=1，则VP-MAC=VA-PCM═

1

3

×

1

2

•PC•PM•h=

1

6

×1×1×

3

2

=

3

12

．（12分）

点评：本题主要考查二面角的平面角、三棱锥体积等有关知识，考查思维能力和空间想象能力、应用向量知识解决数学问题的能力、化归转化能力和推理运算能力．