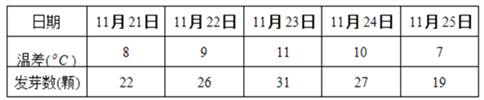
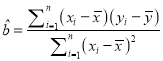题目内容
【题目】椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 为椭圆
为椭圆![]() 上任一点,
上任一点, ![]() 为其右焦点,
为其右焦点, ![]() 是椭圆的左、右顶点,点
是椭圆的左、右顶点,点![]() 满足
满足![]() .
.
①证明: ![]() 为定值;
为定值;
②设![]() 是直线
是直线![]() 上的任一点,直线
上的任一点,直线![]() 分别另交椭圆
分别另交椭圆![]() 于
于![]() 两点,求
两点,求![]() 的最小值.
的最小值.
【答案】(1) ![]() ;(2)①.证明见解析;②.3.
;(2)①.证明见解析;②.3.
【解析】试题分析:(1)将点坐标代人椭圆方程,与离心率联立方程组解得a.b,(2)①根据两点间距离公式,代入椭圆方程化简可得![]() ,再求比值即可,②先设
,再求比值即可,②先设![]() ,根据点斜式可得直线
,根据点斜式可得直线![]() ,
, ![]() 方程,分别与椭圆方程联立解得
方程,分别与椭圆方程联立解得![]() 两点坐标,再根据焦半径公式可得
两点坐标,再根据焦半径公式可得![]() ,最后根据基本不等式求最小值.
,最后根据基本不等式求最小值.
试题解析:(1)由![]() 得
得![]() ,
,
把点![]() 代入椭圆方程为
代入椭圆方程为![]() ,∴
,∴![]() 得
得![]() ,
,
∴![]() ,椭圆的标准方程为
,椭圆的标准方程为![]() ;
;
(2)由(1)知![]() ,
,
 ,
,
而![]() ,∴
,∴ 为定值;
为定值;
②设![]() 若
若![]() ,则
,则![]() ,
,
若![]() ,因为
,因为![]() ,
,
直线![]() ,直线
,直线![]() ,
,
由 整理得
整理得![]() ,
,
∴![]() ,得
,得![]() ,
,
由 整理得
整理得![]() ,
,
∴![]() ,得
,得![]() ,
,
由①知![]() ,
,
∴ ,
,
∵![]() (当且仅当
(当且仅当![]() 即
即![]() 时取等号)
时取等号)
∴ ,即
,即![]() 的最小值为3.
的最小值为3.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
【题目】抢“微信红包”已经成为中国百姓欢度春节时非常喜爱的一项活动.小明收集班内20名同学今年春节期间抢到红包金额![]() (元)如下(四舍五入取整数):
(元)如下(四舍五入取整数):
102 52 41 121 72
162 50 22 158 46
43 136 95 192 59
99 22 68 98 79
对这20个数据进行分组,各组的频数如下:
组别 | 红包金额分组 | 频数 |
|
| 2 |
|
| 9 |
|
|
|
|
| 3 |
|
|
|
(Ⅰ)写出的值,并回答这20名同学抢到的红包金额的中位数落在哪个组别;
(Ⅱ)记![]() 组红包金额的平均数与方差分别为
组红包金额的平均数与方差分别为![]() 组红包金额的平均数与方差分别为
组红包金额的平均数与方差分别为![]() ,试分别比较
,试分别比较![]() 与
与![]() 、
、![]() 与
与![]() 的大小;(只需写出结论)
的大小;(只需写出结论)
(Ⅲ)从![]() 两组的所有数据中任取2个数据,记这2个数据差的绝对值为
两组的所有数据中任取2个数据,记这2个数据差的绝对值为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.