题目内容
设集合 ,集合B是f(x)=ln(1-|x|)的定义域,则A∪B
,集合B是f(x)=ln(1-|x|)的定义域,则A∪B
- A.[
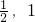 ]
] - B.(-1,2]
- C.(-1,1)∪(1,2)
- D.(-1,2)
D
分析:首先通过解分式不等式化简集合A,然后求出对数型函数的定义域得到集合B,直接取并集.
解答:由 ,得
,得 ,
,
所以A={x| }={x|
}={x| },
},
由1-|x|>0,得-1<x<1,
所以B={x|-1<x<1}.
所以A∪B={x| }∪{x|-1<x<1}=(-1,2).
}∪{x|-1<x<1}=(-1,2).
故选D.
点评:本题考查了并集及其运算,属于以数轴为工具,求集合的并集的基础题,也是高考常考的题型.
分析:首先通过解分式不等式化简集合A,然后求出对数型函数的定义域得到集合B,直接取并集.
解答:由
 ,得
,得 ,
,所以A={x|
 }={x|
}={x| },
},由1-|x|>0,得-1<x<1,
所以B={x|-1<x<1}.
所以A∪B={x|
 }∪{x|-1<x<1}=(-1,2).
}∪{x|-1<x<1}=(-1,2).故选D.
点评:本题考查了并集及其运算,属于以数轴为工具,求集合的并集的基础题,也是高考常考的题型.

练习册系列答案
相关题目
 ,集合B是f(x)=ln(1-|x|)的定义域,则A∪B .
,集合B是f(x)=ln(1-|x|)的定义域,则A∪B . ,集合B是f(x)=ln(1-|x|)的定义域,则A∪B( )
,集合B是f(x)=ln(1-|x|)的定义域,则A∪B( ) ]
] ,集合B是f(x)=ln(1-|x|)的定义域,则A∪B .
,集合B是f(x)=ln(1-|x|)的定义域,则A∪B . ,集合B是f(x)=ln(1-|x|)的定义域,则A∪B( )
,集合B是f(x)=ln(1-|x|)的定义域,则A∪B( ) ]
]