题目内容

已知f(x)=ax2+bx+c,对于x∈［-1,1］,总有|f(x)|≤1,求证:|2a+b|≤4.

证明:∵x∈［-1,1］,|f(x)|≤1,?

∴|f(1)|=|a+b+c|≤1,

f(0)=|c|≤1,?

f(-1)=|a-b+c|≤1.?

令2a+b=Mf(1)+Nf(0)+Pf(-1),?

即2a+b=M(a+b+c)+Nc+P(a-b+c)?

=(M+P)a+(M-P)b+(M+N+P)c,?

∴∴

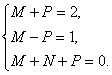∴|2a+b|=|f(1)-2f(0)+f(-1)|≤|f(1)|+2|f(0)|+|f(-1)|?

∴|2a+b|=|f(1)-2f(0)+ f(-1)|≤+2+=4.

练习册系列答案
相关题目
已知f(x)=
ax2+x
2x2+b
为奇函数（a，b是常数），且函数f（x）的图象过点(1，
1
3
)
（1）求f（x）的表达式；
（2）定义正数数列{an}，a1=
1
2
，
a
2
n+1
=2anf(an)(n∈N*)，求数列{an2}的通项公式；
（3）已知b&n=
a
2
n
a
2
n+1
2n-2
，设Sn为bn的前n项和，证明：
1
6
≤Sn＜
1
2
．
已知f(x)=
ax2+x
2x2+b
（a，b为常数）为奇函数，且过点(1，
1
3
)．
（1）求f（x）的表达式；
（2）定义正数数列{an}，a1=
1
2
，
a
2
n+1
=2anf(an)(n∈N*)，证明：数列{
1
a
2
n
-2}是等比数列；
（3）令bn=
1
a
2
n
-2，Sn为{bn}的前n项和，求使Sn＞
31
8
成立的最小n值．
已知f(x)=
ax2+2
b-3x
是定义在（-∞，0）∪（0，+∞）上的奇函数，f(2)=-
5
3
．
（1）求a，b的值；
（2）请用函数单调性的定义说明：f（x）在区间（1，+∞）上的单调性；
（3）求f（x）的值域．
已知f(x)=
ax2+bx+1
x+c
(a＞0)是奇函数，且当x＞0时，f（x）有最小值2
2
，求f（x）的表达式．
已知f(x)=ax2+bx+c(a＞0)的图象与x轴有两个不同的交点，且f(c)=0,当0＜x＜c时，f(x)＞0.

（1）求证：＞c;

（2）求证：-2＜b＜-1;

（3）当c＞1,t＞0时，求证：++＞0.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网