题目内容
已知三个点 .
.
(Ⅰ)求证: ;
;
(Ⅱ)要使四边形 为矩形,求点
为矩形,求点 的坐标,并求矩形
的坐标,并求矩形 两对角线所夹锐角的余弦值.
两对角线所夹锐角的余弦值.
解(Ⅰ)证明:A(2,1),B(3,2),D(-1,4).
∴ =(1,1),
=(1,1), =(-3,3).
=(-3,3).
又∵ =1×(-3)+1×3=0,
=1×(-3)+1×3=0,
∴ .
.
(Ⅱ)∵ ,若四边形ABCD为矩形,则
,若四边形ABCD为矩形,则 .
.
设C点的坐标为(x,y),则有(1,1)=(x+1,y-4),
∴ ∴
∴
∴点C的坐标为(0,5).
由于 =(-2,4),
=(-2,4), =(-4,2),
=(-4,2),
∴ =(-2)×(-4)+4×2=16,
=(-2)×(-4)+4×2=16, =2
=2 .
.
设对角线AC与BD的夹角为θ,则cosθ= =
= >0.
>0.
故矩形ABCD两条对角线所夹锐角的余弦值为 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
, ,
, 则s1,s2,s3的大小关系为( )
则s1,s2,s3的大小关系为( ) s2<s1<s3
s2<s1<s3  s2<s3<s1
s2<s3<s1  s3<s2<s1
s3<s2<s1  ,
, ,
, ,则
,则 等于
等于 B.
B. C.
C. D.
D.
 的一部分图象如右图所示,如果
的一部分图象如右图所示,如果 ,
, _。
_。 ,则
,则 的
的 上的函数
上的函数 是它的导函数,且恒有
是它的导函数,且恒有 成立,则
成立,则

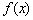 对任意实数x、y满足
对任意实数x、y满足 ,
,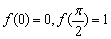 .给出下列结论:①
.给出下列结论:①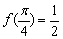 ②
②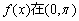 内单调递减
内单调递减