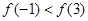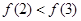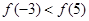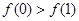题目内容
如果奇函数f(x)在区间[3,7]上是增函数且最大值为5,那么f(x)在区间[-7,-3]上是( )
| A.增函数且最小值是-5 | B.增函数且最大值是-5 |
| C.减函数且最大值是-5 | D.减函数且最小值是-5 |
A
解析试题分析:由奇函数的性质可得函数在区间[3,7]上是增函数且最大值为5. 那么 在区间[-7,-3]上的图像关于原点对称,所以也是递增并且最小值为-5.故选A.本小题主要考查奇函数的图像是关于原点对称的知识.即可得单调性结论.
在区间[-7,-3]上的图像关于原点对称,所以也是递增并且最小值为-5.故选A.本小题主要考查奇函数的图像是关于原点对称的知识.即可得单调性结论.
考点:1.奇函数的性质.2.函数的单调性.3.函数的最值问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
己知函数f(x)= 在[-1,1]上的最大值为M(a) ,若函数g(x)=M(x)-
在[-1,1]上的最大值为M(a) ,若函数g(x)=M(x)- 有4个零点,则实数t的取值范围为( )
有4个零点,则实数t的取值范围为( )
A.(1, ) ) | B.( 1,-1) 1,-1) |
C.( 1,-1) 1,-1) (1, (1,  ) ) | D.( 1,-1) 1,-1) (1,2) (1,2) |
函数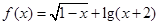 的定义域为
的定义域为
A.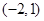 | B.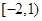 | C.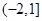 | D.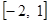 |
函数图象和方程的曲线有密切的关系,如把抛物线 的图象绕远点沿逆时针方向旋转
的图象绕远点沿逆时针方向旋转 就得到函数
就得到函数 的图象,若把双曲线
的图象,若把双曲线 的图象绕原点逆时针方向旋转一定的角度
的图象绕原点逆时针方向旋转一定的角度 后,就得到某一函数的图象,则旋转角
后,就得到某一函数的图象,则旋转角 可以是( )
可以是( )
A. | B. | C. | D. |
定义在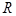 上的函数
上的函数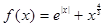 ,且
,且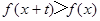 在
在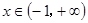 上恒成立,则关于
上恒成立,则关于 的方程
的方程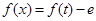 的根的个数叙述正确的是( )
的根的个数叙述正确的是( )
| A.有两个 | B.有一个 | C.没有 | D.上述情况都有可能 |
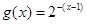 在同一直角坐标系下的图像大致是 ( )
在同一直角坐标系下的图像大致是 ( )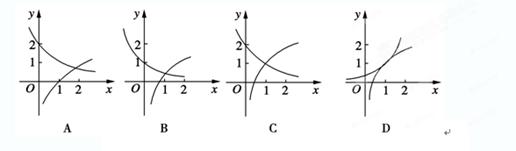
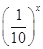 ,在x∈[0,4]上解的个数是( )
,在x∈[0,4]上解的个数是( ) 在
在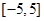 上是偶函数,且在
上是偶函数,且在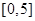 上是单调函数,若
上是单调函数,若 ,则下列不等式一定成立的是( )
,则下列不等式一定成立的是( )