题目内容
已知曲线 的极坐标方程是
的极坐标方程是 ,直线的参数方程是
,直线的参数方程是 (为参数).
(为参数).
设直线与 轴的交点是
轴的交点是 ,
, 是曲线
是曲线 上一动点,求
上一动点,求 的最大值.
的最大值.

解析试题分析:首先将曲线 的极坐标方程、直线的参数方程转化为直角坐标方程,可知,曲线
的极坐标方程、直线的参数方程转化为直角坐标方程,可知,曲线 是以
是以 为圆心,1为半径的圆,由直线的直角坐标方程得,令
为圆心,1为半径的圆,由直线的直角坐标方程得,令 ,可求出点
,可求出点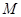 的坐标,则点
的坐标,则点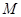 与圆心
与圆心 的距离
的距离 可以求,从而可得曲线
可以求,从而可得曲线 上的动点
上的动点 与定点
与定点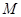 的最大值为
的最大值为 .
.
试题解析:曲线 的直角坐标方程为
的直角坐标方程为 ,故圆
,故圆 的圆心坐标为(0,1),半径
的圆心坐标为(0,1),半径
直线l的直角坐标方程 , 令
, 令 ,得
,得 ,即
,即 点的坐标为(2,0).
点的坐标为(2,0).
从而 ,所以
,所以 .即
.即 的最大值为
的最大值为 。
。
考点:1.圆的极坐标方程;2.直线的参数方程;3.定点到动点的最大值.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 中,直线
中,直线 的参数方程是
的参数方程是 (参数
(参数 ).圆
).圆 的参数方程为
的参数方程为 (参数
(参数 的参数方程是
的参数方程是 (t为参数),曲线C的极坐标方程是
(t为参数),曲线C的极坐标方程是 ,则
,则 ,点P的轨迹为曲线C.
,点P的轨迹为曲线C. 为参数,求曲线C的参数方程;
为参数,求曲线C的参数方程; 距离的最大值.
距离的最大值. (φ为参数)的右焦点,且与直线
(φ为参数)的右焦点,且与直线 (t为参数)平行的直线的普通方程.
(t为参数)平行的直线的普通方程.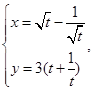 (
( 为参数,
为参数,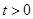 ).求曲线C的普通方程。
).求曲线C的普通方程。 =1上找一点,使这一点到直线x-2y-12=0的距离最小.
=1上找一点,使这一点到直线x-2y-12=0的距离最小. ,(t为参数),求直线的斜率.
,(t为参数),求直线的斜率.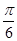 .
.