题目内容
在四面体ABCD中，已知棱AC的长为
，其余各棱长都为2，则二面角A-BD-C的大小为
．
| 6 |
| π |
| 2 |
| π |
| 2 |
分析：取BD的中点E，连接AE、CE，证明∠AEC就是A-BD-C的二面角，解三角形ACE即可得到二面角A-BD-C的大小．
解答：
解：取BD的中点E，连接AE、CE
∵AB=AD=BC=CD，
∴CE⊥BD，AE⊥BD
∴∠AEC就是A-BD-C的二面角
∵AB=AD=BD=BC=CD=2，
∴AE=CE=
∵AC=
∴∠AEC=
即二面角A-BD-C的大小为
故答案为：
．
解：取BD的中点E，连接AE、CE∵AB=AD=BC=CD，
∴CE⊥BD，AE⊥BD
∴∠AEC就是A-BD-C的二面角
∵AB=AD=BD=BC=CD=2，
∴AE=CE=
| 3 |
∵AC=
| 6 |
∴∠AEC=
| π |
| 2 |
即二面角A-BD-C的大小为
| π |
| 2 |
故答案为：
| π |
| 2 |
点评：本题考查二面角的平面角及求法，其中构造出二面角A-BD-C的平面角∠AEC是解答本题的关键．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
在四面体ABCD中，设AB=1，CD=2且AB⊥CD，若异面直线AB与CD间的距离为2，则四面体ABCD的体积为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
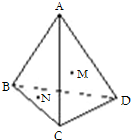在四面体ABCD中，M、N分别是面△ACD、△BCD的重心，则四面体的四个面中与MN平行的是
将图1中的等腰直角三角形ABC沿斜边BC的中线折起得到四面体ABCD（如图2），则在四面体ABCD中，AD与BC的位置关系是（ ）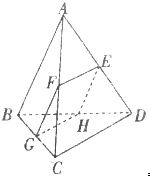
如图，在四面体ABCD中，截面EFGH平行于对棱AB和CD，且FG⊥GH，试问截面在什么位置时其截面面积最大．