题目内容
已知椭圆C: (a>b>0)上的任意一点到它的两个焦点(-c,0),(c,0)的距离之和为
(a>b>0)上的任意一点到它的两个焦点(-c,0),(c,0)的距离之和为 ,且它的焦距为2。
,且它的焦距为2。
(1)求椭圆C的方程;
(2)已知直线x-y+m=0与椭圆C交于不同的两点A,B,且线段AB的中点不在圆 内,求m的取值范围。
内,求m的取值范围。
 (a>b>0)上的任意一点到它的两个焦点(-c,0),(c,0)的距离之和为
(a>b>0)上的任意一点到它的两个焦点(-c,0),(c,0)的距离之和为 ,且它的焦距为2。
,且它的焦距为2。(1)求椭圆C的方程;
(2)已知直线x-y+m=0与椭圆C交于不同的两点A,B,且线段AB的中点不在圆
 内,求m的取值范围。
内,求m的取值范围。解:(1)依题意可知
又∵b2=a2-c2,
解得
则椭圆方程为 。
。
(2)联立方程
消去y整理得:3x2+4mx+2m2-2=0
则Δ=16m2-12(2m2-2)=8(-m2+3)>0,
解得
设A(x1,y1),B(x2,y2),
则

即AB的中点为
又∵AB的中点不在 内,
内,
∴
解得m≤-1或m≥1 ②
由①②得: 或
或 。
。

又∵b2=a2-c2,
解得

则椭圆方程为
 。
。(2)联立方程

消去y整理得:3x2+4mx+2m2-2=0
则Δ=16m2-12(2m2-2)=8(-m2+3)>0,
解得

设A(x1,y1),B(x2,y2),
则


即AB的中点为

又∵AB的中点不在
 内,
内, ∴

解得m≤-1或m≥1 ②
由①②得:
 或
或 。
。
练习册系列答案
 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
 +
+ =1(a>b>0),直线y=x+
=1(a>b>0),直线y=x+ 与以原点为圆心,以椭圆C的短半轴长为半径
与以原点为圆心,以椭圆C的短半轴长为半径 ,0)求实数k的取值范围。
,0)求实数k的取值范围。 +
+ =1(a>b>0),直线y=x+
=1(a>b>0),直线y=x+ 与以原点为圆心,以椭圆C的短半轴长为半径的圆相切,F1,F2为其左、右焦点,P为椭圆C上任一点,△F1PF2的重心为G,内心为I,且IG∥F1F2。⑴求椭圆C的方程。⑵若直线L:y=kx+m(k≠0)与椭圆C交于不同两点A,B且线段AB的垂直平分线过定点C(
与以原点为圆心,以椭圆C的短半轴长为半径的圆相切,F1,F2为其左、右焦点,P为椭圆C上任一点,△F1PF2的重心为G,内心为I,且IG∥F1F2。⑴求椭圆C的方程。⑵若直线L:y=kx+m(k≠0)与椭圆C交于不同两点A,B且线段AB的垂直平分线过定点C( ,0)求实数k的取值范围。
,0)求实数k的取值范围。 (a>b>0),直线y=x+
(a>b>0),直线y=x+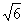 与以原点为圆心,以椭圆C的短半轴长为半径的圆相切,F1、F2为其左、右焦点,P为椭圆C上任一点,△F1PF2的重心为G,内心为I,且IG∥F1F2。
与以原点为圆心,以椭圆C的短半轴长为半径的圆相切,F1、F2为其左、右焦点,P为椭圆C上任一点,△F1PF2的重心为G,内心为I,且IG∥F1F2。 ,0),求实数k的取值范围。
,0),求实数k的取值范围。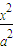 +
+ (a>b>0)的焦距为4,且过点P(
(a>b>0)的焦距为4,且过点P( ,
, ).
). ),连接AE,过点A作AE的垂线交x轴于点D.点G是点D关于y轴的对称点,作直线QG,问这样作出的直线QG是否与椭圆C一定有唯一的公共点?并说明理由.
),连接AE,过点A作AE的垂线交x轴于点D.点G是点D关于y轴的对称点,作直线QG,问这样作出的直线QG是否与椭圆C一定有唯一的公共点?并说明理由. (a>b>0),直线l过点A(a,0)和
(a>b>0),直线l过点A(a,0)和