题目内容
已知椭圆C : (a>b>0),直线y=x+
(a>b>0),直线y=x+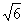 与以原点为圆心,以椭圆C的短半轴长为半径的圆相切,F1、F2为其左、右焦点,P为椭圆C上任一点,△F1PF2的重心为G,内心为I,且IG∥F1F2。
与以原点为圆心,以椭圆C的短半轴长为半径的圆相切,F1、F2为其左、右焦点,P为椭圆C上任一点,△F1PF2的重心为G,内心为I,且IG∥F1F2。
(1)求椭圆C的方程;
(2)若直线L:y=kx+m(k≠0)与椭圆C交于不同两点A,B且线段AB的垂直平分线过定点C( ,0),求实数k的取值范围。
,0),求实数k的取值范围。
 (a>b>0),直线y=x+
(a>b>0),直线y=x+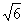 与以原点为圆心,以椭圆C的短半轴长为半径的圆相切,F1、F2为其左、右焦点,P为椭圆C上任一点,△F1PF2的重心为G,内心为I,且IG∥F1F2。
与以原点为圆心,以椭圆C的短半轴长为半径的圆相切,F1、F2为其左、右焦点,P为椭圆C上任一点,△F1PF2的重心为G,内心为I,且IG∥F1F2。(1)求椭圆C的方程;
(2)若直线L:y=kx+m(k≠0)与椭圆C交于不同两点A,B且线段AB的垂直平分线过定点C(
 ,0),求实数k的取值范围。
,0),求实数k的取值范围。解:(1)设P(x0,y0),x0 ±a,则G(
±a,则G( ,
, ),
),
∵IG∥F1F2,
∴Iy= ,|F1F2|=2c,
,|F1F2|=2c,
∴ =
= ·|F1F2|·|y0|=
·|F1F2|·|y0|= (|PF1|+|PF2|+|F1F2|)·|
(|PF1|+|PF2|+|F1F2|)·| |,
|,
∴2c·3=2a+2c,
∴e= =
= ,
,
又∵b=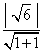 ,
,
∴b= ,
,
∴a=2,
∴椭圆C的方程为 +
+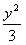 =1。
=1。
(2)设A(x1,y1)、B(x2,y2),
 ,消去y得(3+4k2)x2+8kmx+4m2-12=0,
,消去y得(3+4k2)x2+8kmx+4m2-12=0,
∴△=(8km)2-4(3+4k2)(4m2-12)>0,
即m2<4k2+3,
又∵x1+x2=- ,则y1+y2=
,则y1+y2= ,
,
∴线段AB的中点P的坐标为(- ,
, ),
),
又线段AB的垂直平分线l′的方程为y= (x-
(x- ),
),
点P在直线l′上, =
= (
( ),
),
∴4k2+6km+3=0,
∴m= (4k2+3),
(4k2+3),
∴ <4k2+3,
<4k2+3,
∴k2> ,
,
∴k> 或k>
或k> ,
,
∴k的取值范围是(-∞, )∪(
)∪( ,+∞)。
,+∞)。
 ±a,则G(
±a,则G( ,
, ),
),∵IG∥F1F2,
∴Iy=
 ,|F1F2|=2c,
,|F1F2|=2c,∴
 =
= ·|F1F2|·|y0|=
·|F1F2|·|y0|= (|PF1|+|PF2|+|F1F2|)·|
(|PF1|+|PF2|+|F1F2|)·| |,
|,∴2c·3=2a+2c,
∴e=
 =
= ,
, 又∵b=
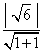 ,
, ∴b=
 ,
,∴a=2,
∴椭圆C的方程为
 +
+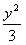 =1。
=1。(2)设A(x1,y1)、B(x2,y2),
 ,消去y得(3+4k2)x2+8kmx+4m2-12=0,
,消去y得(3+4k2)x2+8kmx+4m2-12=0,∴△=(8km)2-4(3+4k2)(4m2-12)>0,
即m2<4k2+3,
又∵x1+x2=-
 ,则y1+y2=
,则y1+y2= ,
,∴线段AB的中点P的坐标为(-
 ,
, ),
), 又线段AB的垂直平分线l′的方程为y=
 (x-
(x- ),
), 点P在直线l′上,
 =
= (
( ),
),∴4k2+6km+3=0,
∴m=
 (4k2+3),
(4k2+3), ∴
 <4k2+3,
<4k2+3, ∴k2>
 ,
, ∴k>
 或k>
或k> ,
, ∴k的取值范围是(-∞,
 )∪(
)∪( ,+∞)。
,+∞)。
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ),两个焦点为(-1,0)(1,0)。
),两个焦点为(-1,0)(1,0)。