题目内容
设F1、F2是曲线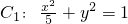 的焦点,P是曲线
的焦点,P是曲线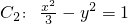 与C1的一个交点,则cos∠F1PF2的值为
与C1的一个交点,则cos∠F1PF2的值为
- A.等于零
- B.大于零
- C.小于零
- D.以上三种情况都有可能
A
分析:先根据曲线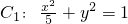 的得出其焦点,再联立方程组求出P的坐标,由此求出
的得出其焦点,再联立方程组求出P的坐标,由此求出  ,最后根据向量的夹角公式进行求解即可.
,最后根据向量的夹角公式进行求解即可.
解答:由题意知F1(-2,0),F2(2,0),
解方程组 得
得  ,
,
取P点坐标为( ),
), ,
,
 =0,
=0,
cos∠F1PF2=0.
故选A.
点评:本题考查双曲线和椭圆的定义和标准方程,以及简单性质的应用,考查数形结合思想,属于基础题.
分析:先根据曲线
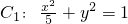 的得出其焦点,再联立方程组求出P的坐标,由此求出
的得出其焦点,再联立方程组求出P的坐标,由此求出  ,最后根据向量的夹角公式进行求解即可.
,最后根据向量的夹角公式进行求解即可.解答:由题意知F1(-2,0),F2(2,0),
解方程组
 得
得  ,
,取P点坐标为(
 ),
), ,
,
 =0,
=0,cos∠F1PF2=0.
故选A.
点评:本题考查双曲线和椭圆的定义和标准方程,以及简单性质的应用,考查数形结合思想,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
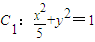 的焦点,P是曲线
的焦点,P是曲线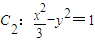 与C1的一个交点,则cos∠F1PF2的值为( )
与C1的一个交点,则cos∠F1PF2的值为( )