题目内容
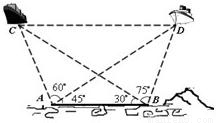
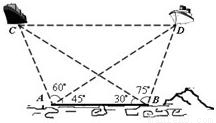
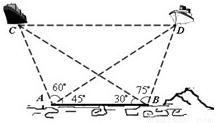
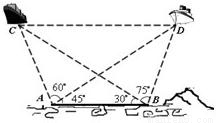
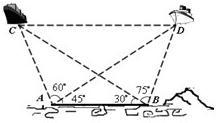 已知海岸边A,B两海事监测站相距60nmile,为了测量海平面上两艘油轮C,D间距离,在A,B两处分别测得∠CBD=75°,∠ABC=30°,∠DAB=45°,∠CAD=60°(A,B,C,D在同一个水平面内).请计算出C,D两艘轮船间距离.
已知海岸边A,B两海事监测站相距60nmile,为了测量海平面上两艘油轮C,D间距离,在A,B两处分别测得∠CBD=75°,∠ABC=30°,∠DAB=45°,∠CAD=60°(A,B,C,D在同一个水平面内).请计算出C,D两艘轮船间距离.
分析:在△ABD中先利用正弦定理求得AD,在△ABC中求得AC,然后在△ACD中,应用余弦定理求得CD.
解答:解:在△ABD中,由正弦定理得:
=
,
∴AD=
=
=
=30(
+
)
同理,在△ABC中,由正弦定理得:
=
AC=
=
=
=30
在△ACD中,应用余弦定理计算出CD两点间的距离:
CD=
=
=
=
=30
∴C,D两艘轮船相距30
nmile.
| AD |
| sin∠ABD |
| AB |
| sin∠ADB |
∴AD=
| 60sin(30°+75°) |
| sin[180°-(45°+30°+75°)] |
| 60sin75° |
| sin30° |
60×
| ||||||
|
| 6 |
| 2 |
同理,在△ABC中,由正弦定理得:
| AC |
| sin∠ABC |
| AB |
| sin∠ACB |
| 60sin30° |
| sin[180°-(45°+30°+60°)] |
60×
| ||
| sin45° |
| 30 | ||||
|
| 2 |
在△ACD中,应用余弦定理计算出CD两点间的距离:
CD=
| AC2+AD2-2AC•AD•cos60° |
=
900×2+900(
|
=
900×8+3600
|
=
7200+1800
|
=30
8+2
|
∴C,D两艘轮船相距30
8+2
|
点评:本题主要考查了解三角形的实际应用,正弦定理和余弦定理的综合运用.考查了三角函数基础知识的综合把握.

练习册系列答案
相关题目