Question

【题目】如图，已知矩形中， 、分别是、上的点， ，，是的中点，现沿着翻折,使平面平面.

（Ⅰ）为的中点，求证：平面.

（Ⅱ）求异面直线与所成角的大小.

Answer 1

【答案】（1）见解析；（2）异面直线AD与BC的所成角为.

【解析】

（1）取的中点，根据线面平行判定定理得∥平面，∥平面，再根据面面平行判定定理得平面∥平面,最后得结论，（2）先根据等腰三角形性质得AP⊥DE,再根据面面垂直性质定理得⊥平面，最后根据等体积法求点到平面的距离.

（Ⅰ）取的中点，连接,，易证∥,

∴∥平面.

∵是△的中位线，∴∥,

,∴∥平面.

,

∴平面∥平面, ∥平面.

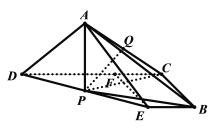
（Ⅱ）连接AP、PB，∵AD=AE,点P为DE的中点，∴AP⊥DE,

∵平面ADE⊥平面BCDE,平面平面 ,

⊥平面，⊥.

根据余弦定理可求得 ,

同理可求得 ,

同理可求得 , , ，

三棱锥 的高为 , ,设点P到平面距离为d, , ， ．