题目内容
已知函数y=sinx+acosx的图象关于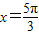 对称,则函数y=asinx+cosx的图象的一条对称轴是( )
对称,则函数y=asinx+cosx的图象的一条对称轴是( )A.x=
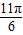
B.x=
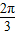
C.x=
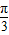
D.x=π
【答案】分析:函数y=sinx+acosx变为y=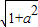 sin(x+∅),tan∅=a又图象关于
sin(x+∅),tan∅=a又图象关于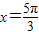 对称,
对称,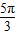 +∅=kπ+
+∅=kπ+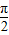 ,k∈z,可求得∅=kπ-
,k∈z,可求得∅=kπ-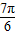 ,由此可求得a=tan∅=tan(kπ-
,由此可求得a=tan∅=tan(kπ-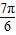 )=-
)=-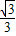 ,将其代入函数y=asinx+cosx化简后求对称轴即可.
,将其代入函数y=asinx+cosx化简后求对称轴即可.
解答:解:y=sinx+acosx变为y=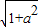 sin(x+∅),(令tan∅=a)又
sin(x+∅),(令tan∅=a)又
图象关于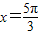 对称,
对称,
∴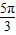 +∅=kπ+
+∅=kπ+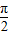 ,k∈z,可求得∅=kπ-
,k∈z,可求得∅=kπ-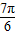 ,
,
由此可求得a=tan∅=tan(kπ-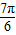 )=-
)=-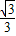 ,
,
函数y=-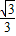 sinx+cosx=
sinx+cosx=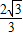 sin(x+θ),(tanθ=-
sin(x+θ),(tanθ=-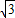 )
)
其对称轴方程是x+θ=kπ+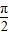 ,k∈z,
,k∈z,
即x=kπ+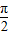 -θ
-θ
又tanθ=-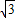 ,故θ=k1π-
,故θ=k1π-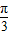 ,k1∈z
,k1∈z
故函数y=asinx+cosx的图象的对称轴方程为x=(k-k1)π+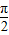 +
+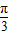 =(k-k1)π+
=(k-k1)π+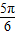 ,k-k1∈z,
,k-k1∈z,
当k-k1=1时,对称轴方程为x=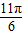
故选A.
点评:本题考查三角恒等变形以及正弦类函数的对称性质,是三角函数中综合性比较强的题目,比较全面地考查了三角函数的图象与性质.
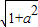 sin(x+∅),tan∅=a又图象关于
sin(x+∅),tan∅=a又图象关于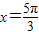 对称,
对称,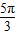 +∅=kπ+
+∅=kπ+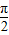 ,k∈z,可求得∅=kπ-
,k∈z,可求得∅=kπ-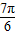 ,由此可求得a=tan∅=tan(kπ-
,由此可求得a=tan∅=tan(kπ-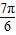 )=-
)=-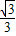 ,将其代入函数y=asinx+cosx化简后求对称轴即可.
,将其代入函数y=asinx+cosx化简后求对称轴即可.解答:解:y=sinx+acosx变为y=
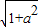 sin(x+∅),(令tan∅=a)又
sin(x+∅),(令tan∅=a)又图象关于
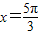 对称,
对称,∴
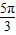 +∅=kπ+
+∅=kπ+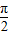 ,k∈z,可求得∅=kπ-
,k∈z,可求得∅=kπ-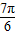 ,
,由此可求得a=tan∅=tan(kπ-
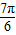 )=-
)=-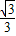 ,
,函数y=-
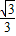 sinx+cosx=
sinx+cosx=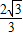 sin(x+θ),(tanθ=-
sin(x+θ),(tanθ=-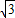 )
)其对称轴方程是x+θ=kπ+
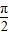 ,k∈z,
,k∈z,即x=kπ+
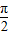 -θ
-θ又tanθ=-
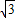 ,故θ=k1π-
,故θ=k1π-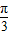 ,k1∈z
,k1∈z故函数y=asinx+cosx的图象的对称轴方程为x=(k-k1)π+
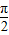 +
+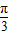 =(k-k1)π+
=(k-k1)π+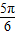 ,k-k1∈z,
,k-k1∈z,当k-k1=1时,对称轴方程为x=
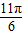
故选A.
点评:本题考查三角恒等变形以及正弦类函数的对称性质,是三角函数中综合性比较强的题目,比较全面地考查了三角函数的图象与性质.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目