题目内容
已知函数
(1)求函数f(x)在[-π,0]上的单调区间;
(2)已知角α满足 ,
, ,求f(α)的值.
,求f(α)的值.
解:(1)∵ ,
,
故 函数f(x)在区间 单调递减,在区间
单调递减,在区间 单调递增.
单调递增.
(2)∵ ,
, ,∴
,∴ ,
,
∴2sinαcosα+2(cos2α-sin2α)=1,∴cos2α+2sinαcosα-3sin2α=0,∴(cosα+3sinα)(cosα-sinα)=0,
∴cosα-sinα=0,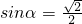 ,∴
,∴ .
.
分析:(1)化简函数f(x)的解析式为 sinx,利用正弦函数的单调性求出函数f(x)在[-π,0]上的单调区间.
sinx,利用正弦函数的单调性求出函数f(x)在[-π,0]上的单调区间.
(2)由 ,化简已知的等式可得(cosα+3sinα)(cosα-sinα)=0,故有cosα-sinα=0,
,化简已知的等式可得(cosα+3sinα)(cosα-sinα)=0,故有cosα-sinα=0,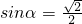 ,从而得到
,从而得到 的值.
的值.
点评:本题考查二倍角公式,正弦函数的单调性,三角函数的化简求值,求出函数f(x)的解析式,是解题的突破口.
 ,
,故 函数f(x)在区间
 单调递减,在区间
单调递减,在区间 单调递增.
单调递增.(2)∵
 ,
, ,∴
,∴ ,
,∴2sinαcosα+2(cos2α-sin2α)=1,∴cos2α+2sinαcosα-3sin2α=0,∴(cosα+3sinα)(cosα-sinα)=0,
∴cosα-sinα=0,
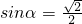 ,∴
,∴ .
.分析:(1)化简函数f(x)的解析式为
 sinx,利用正弦函数的单调性求出函数f(x)在[-π,0]上的单调区间.
sinx,利用正弦函数的单调性求出函数f(x)在[-π,0]上的单调区间.(2)由
 ,化简已知的等式可得(cosα+3sinα)(cosα-sinα)=0,故有cosα-sinα=0,
,化简已知的等式可得(cosα+3sinα)(cosα-sinα)=0,故有cosα-sinα=0,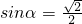 ,从而得到
,从而得到 的值.
的值.点评:本题考查二倍角公式,正弦函数的单调性,三角函数的化简求值,求出函数f(x)的解析式,是解题的突破口.

练习册系列答案
相关题目



 的极值点;
的极值点; 过点(0,—1),并且与曲线
过点(0,—1),并且与曲线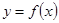 相切,求直线
相切,求直线 ,其中
,其中 ,求函数
,求函数 在
在 上的最小值.(其中e为自然对数的底数)
上的最小值.(其中e为自然对数的底数)