题目内容
设P是双曲线 上的一点,F1、F2分别是双曲线的左、右焦点,则以线段PF2为直径的圆与以双曲线的实轴为直径的圆的位置关系是( )
上的一点,F1、F2分别是双曲线的左、右焦点,则以线段PF2为直径的圆与以双曲线的实轴为直径的圆的位置关系是( )A.内切
B.外切
C.内切或外切
D.不相切
【答案】分析:利用双曲线的定义,通过圆心距判断出当点P分别在左、右两支时,两圆相内切、外切.
解答: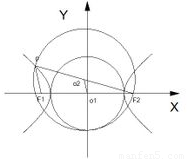 解:设以实轴|F1F2|为直径的圆的圆心为O1,其半径r1=a,
解:设以实轴|F1F2|为直径的圆的圆心为O1,其半径r1=a,
线段PF2为直径的圆的圆心为O2,其半径为r2=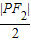 ,
,
当P在双曲线左支上时,
|O1O2|=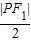 ,
,
∵r2-|O1O2|=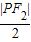 -
-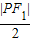 =a=r1,
=a=r1,
∴两圆内切.
当当P在双曲线右支上时,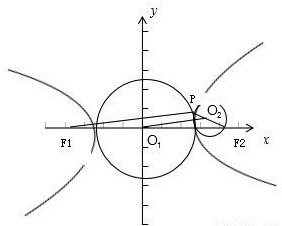
|O1O2|=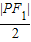 ,
,
∵|O1O2|-r2=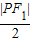 -
-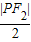 =a=r1,
=a=r1,
∴r1+r2=|O1O2|
∴两圆外切.
故选C.
点评:本题考查直线和双曲线的位置关系,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,易错点是容易只考虑P点在一个分支上而导致丢解,是高考的重点.解题时要认真审题,仔细解答.
解答:
 解:设以实轴|F1F2|为直径的圆的圆心为O1,其半径r1=a,
解:设以实轴|F1F2|为直径的圆的圆心为O1,其半径r1=a,线段PF2为直径的圆的圆心为O2,其半径为r2=
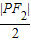 ,
,当P在双曲线左支上时,
|O1O2|=
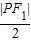 ,
,∵r2-|O1O2|=
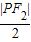 -
-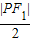 =a=r1,
=a=r1,∴两圆内切.
当当P在双曲线右支上时,

|O1O2|=
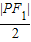 ,
,∵|O1O2|-r2=
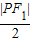 -
-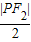 =a=r1,
=a=r1,∴r1+r2=|O1O2|
∴两圆外切.
故选C.
点评:本题考查直线和双曲线的位置关系,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,易错点是容易只考虑P点在一个分支上而导致丢解,是高考的重点.解题时要认真审题,仔细解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设F1,F2是双曲线x2-
=1的两个焦点,P是双曲线上的一点,且3|PF1|=4|PF2|,则△PF1F2的面积等于( )
| y2 |
| 24 |
A、4
| ||
B、8
| ||
| C、24 | ||
| D、48 |