题目内容
若椭圆 的中心在原点,焦点在
的中心在原点,焦点在 轴上,短轴的一个端点与左右焦点
轴上,短轴的一个端点与左右焦点 、
、 组成一个正三角形,焦点到椭圆上的点的最短距离为
组成一个正三角形,焦点到椭圆上的点的最短距离为 .
.
(1)求椭圆 的方程;
的方程;
(2)过点 作直线
作直线 与椭圆
与椭圆 交于
交于 、
、 两点,线段
两点,线段 的中点为
的中点为 ,求直线
,求直线 的斜率
的斜率 的取值范围.
的取值范围.
【答案】
(1)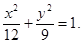 (2)
(2)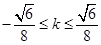 且
且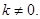
【解析】
试题分析:(1)设椭圆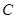 的方程为
的方程为
由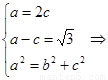
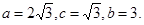 所以,椭圆
所以,椭圆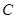 的方程为
的方程为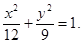 ……1…5
分
……1…5
分
(2) 、
、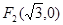 ,
,
当直线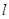 的斜率不存在时,
的斜率不存在时,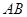 的中点为
的中点为 ,直线
,直线 的斜率
的斜率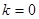 ;
;
当直线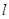 的斜率存在时,设其斜率为
的斜率存在时,设其斜率为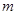 ,直线
,直线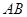 的方程为:
的方程为: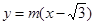 ,……2
,……2
由12联立消去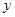 并整理得:
并整理得: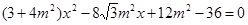
设 ,则
,则 ……10分
……10分
当 时,
时,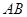 的中点为坐标原点,直线
的中点为坐标原点,直线 的斜率
的斜率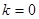 ; ……11
分
; ……11
分
当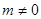 时,
时, ,
,
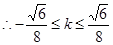 且
且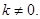 ……13
分
……13
分
考点:椭圆方程性质及直线与椭圆的位置关系
点评:直线与椭圆相交的问题常联立方程,结合韦达定理求解,在求解过程中要注意分直线斜率是否存在两种情况分别讨论,再应用均值不等式求得斜率最值

练习册系列答案
相关题目
 ),求直线l的斜率k的取值范围.
),求直线l的斜率k的取值范围.