题目内容
如图,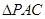 与
与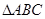 是均以
是均以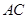 为斜边的等腰直角三角形,
为斜边的等腰直角三角形, ,
,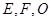 分别为
分别为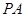 ,
,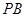 ,
,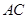 的中点,
的中点,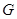 为
为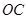 的中点,且
的中点,且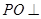 平面
平面 .
.
(1)证明: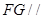 平面
平面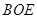 ;
;
(2)求二面角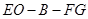 的余弦值.
的余弦值.
(1)以O点为坐标原点, 的方向为
的方向为 正方向建立空间直角坐标系数,
正方向建立空间直角坐标系数, 平面
平面 的法向量为
的法向量为 ,
, ,所以
,所以 ,所以
,所以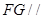 平面
平面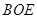 (2)
(2)
解析试题分析:以O点为坐标原点, 的方向为
的方向为 正方向建立空间直角坐标系数,则
正方向建立空间直角坐标系数,则
 设平面
设平面 的法向量为
的法向量为
则 ,令
,令 ,则
,则
所以 ,所以
,所以 ,所以
,所以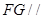 平面
平面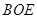 .
.
⑵平面 的法向量为
的法向量为 .设平面
.设平面 的法向量为
的法向量为 ,又
,又 ,则
,则 ,令
,令 ,则
,则
设二面角 的平面角为
的平面角为 ,则
,则
又由图易知二面角 的平面角为锐角,
的平面角为锐角, 二面角
二面角 的余弦值为
的余弦值为
考点:空间线面平行的判定及二面角的求法
点评:本题中利用 两两垂直,空间坐标系较容易建立,因此只需根据线段长度找到点的坐标,进而转化为用直线的方向向量和平面的法向量来判定位置关系或求角
两两垂直,空间坐标系较容易建立,因此只需根据线段长度找到点的坐标,进而转化为用直线的方向向量和平面的法向量来判定位置关系或求角

练习册系列答案
相关题目
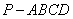 的底面
的底面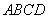 是等腰梯形,
是等腰梯形,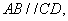 且
且
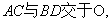

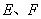 分别是
分别是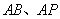 的中点.
的中点.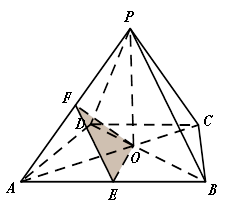
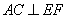 ;
;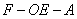 的余弦值.
的余弦值. 
 中,
中, 是棱
是棱 的中点.
的中点.
 平面
平面 ;
; .
.
 是双曲线
是双曲线

 上一点,
上一点, 、
、 分别是双曲线
分别是双曲线 的左、右顶点,直线
的左、右顶点,直线 ,
,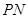 的斜率之积为
的斜率之积为 .
.
 ,
, 两点,
两点, 为坐标原点,
为坐标原点, 为双曲线上一点,满足
为双曲线上一点,满足 ,求
,求 的值.
的值.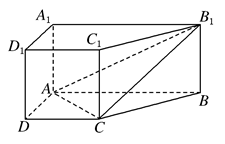
 平面ABCD,AE=EB=BC=2,F为CE上的点,且BF
平面ABCD,AE=EB=BC=2,F为CE上的点,且BF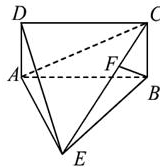
 G是EF的中
G是EF的中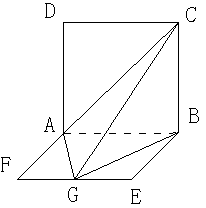
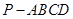 中,
中,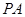 ⊥平面
⊥平面 ,
, 为
为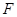 为
为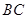 的中点,底面
的中点,底面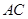 ,
, 交于点
交于点 .
.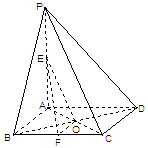
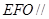 平面
平面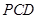 ;
; ⊥平面
⊥平面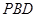 .
.