题目内容
 在直线l:x+y-4=0上任取一点M,过点M且以双曲线x2-
在直线l:x+y-4=0上任取一点M,过点M且以双曲线x2-| y2 | 3 |
(1)M点在何处时,所求椭圆长轴最短;
(2)求长轴最短时的椭圆方程.
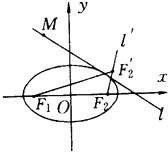
分析:(1)设F2关于l的对称点为F2'(m,n),连结F1F2',由平面几何知识可得F1F2'长就是椭圆长轴的最小值.再根据轴对称的性质,联解直线方程得到M坐标为(
,
),即为满足椭圆长轴最短的点M位置;
(2)由(1)的结论算出2a=|MF1|+|MF′2|=|F1F′2|=2
,可得a=
,再根据椭圆焦点坐标为(±2,O)得c=2,算出b2=6,即可得到所求椭圆方程.
| 5 |
| 2 |
| 3 |
| 2 |
(2)由(1)的结论算出2a=|MF1|+|MF′2|=|F1F′2|=2
| 10 |
| 10 |
解答: 解:(1)双曲线x2-
解:(1)双曲线x2-
=1中,a2=1且b2=3,
∴c2=a2+b2=4,
可得双曲线x2-
=1的两焦点F1(-2,0),F2(2,0),
过F2向l引垂直线l':y=x-2,设F2关于l的对称点为F2'(m,n),
则
,解之得m=4且n=2,得F2'(4,2)(如图),
∴直线F1F2'的方程为
=
,化简得x-3y+2=0.
由
,解得
,
∴M(
,
)即为满足椭圆长轴最短的点;
(2)设所求椭圆方程为
+
=1(a>b>0),
由(1)得椭圆长轴最短时,2a=|MF1|+|MF2|=|MF1|+|MF′2|=|F1F′2|=2
,可得a=
,
∵焦点为(±2,O),得c=2,
∴b2=a2-c2=10-4=6,所求椭圆方程为
+
=1.
 解:(1)双曲线x2-
解:(1)双曲线x2-| y2 |
| 3 |
∴c2=a2+b2=4,
可得双曲线x2-
| y2 |
| 3 |
过F2向l引垂直线l':y=x-2,设F2关于l的对称点为F2'(m,n),
则
|
∴直线F1F2'的方程为
| y-0 |
| 2-0 |
| x+2 |
| 4+2 |
由
|
|
∴M(
| 5 |
| 2 |
| 3 |
| 2 |
(2)设所求椭圆方程为
| x2 |
| a2 |
| y2 |
| b2 |
由(1)得椭圆长轴最短时,2a=|MF1|+|MF2|=|MF1|+|MF′2|=|F1F′2|=2
| 10 |
| 10 |
∵焦点为(±2,O),得c=2,
∴b2=a2-c2=10-4=6,所求椭圆方程为
| x2 |
| 10 |
| y2 |
| 6 |
点评:本题求以定点为焦点,且长轴最短的椭圆的标准方程.着重考查了直线的位置关系、椭圆的标准方程与简单几何性质等知识,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2010•江苏二模)在等腰△ABC中,已知AB=AC,B(-1,0),D(2,0)为AC的中点.
(2010•江苏二模)在等腰△ABC中,已知AB=AC,B(-1,0),D(2,0)为AC的中点.