题目内容
若在直角坐标平面第一象限内,点的坐标(x,y)满足x+y>n,并且x,y都小于n(n∈N*)的整点(横、纵坐标均为整数)的个数记为an.(1)求a3,a4,a5并写出数列{an}的通项公式an=f(n)(不要求证明);
(2)设列数{bn}满足bn=n2-2an,Tn=2n-1b1+2n-2b2+…+2bn-1+bn,求Tn.
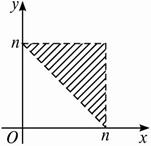
解:(1)满足条件的点(x,y)在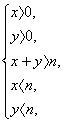 x>0,表示的平面区域内,如图阴影部分.
x>0,表示的平面区域内,如图阴影部分.
 ?
?
∴不难得出a3=1,a4=2,a5=3, ?
an=1+2+3+…+(n-2)?
=![]() . ?
. ?
(2)bn=n2-2an=3n-2, ?
∵bn+1-bn=3.∴数列{bn}是以1为首项,公差为3的等差数列. ?
Tn=2n-1b1+2n-2b2+…+2bn-1+bn?
=2n-1+2n-2·4+…+2(3n-5)+(3n-2), ①?
∴2Tn=2n+2n-1·4+…+22(3n-5)+2(3n-2). ②?
②-①得Tn=2n+3(2n-1+2n-2+…+2)-(3n-2)?
=2n+![]() -3n+2=2n+2-3n-4.?
-3n+2=2n+2-3n-4.?
∴Tn=2n+2-3n-4.

 名校课堂系列答案
名校课堂系列答案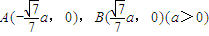 ,两动点M、N满足
,两动点M、N满足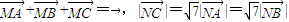 ,向量
,向量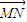 与
与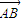 共线.
共线.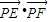 的取值范围.
的取值范围.