Question

已知圆0：x²+y²=1和直线l：y=2x+b交于A、B两点，若A、B分别在角α、β的终边上，则sin（α+β）=

-

4

5

．

Answer 1

分析：如图所示，设A（x₁，y₁），B（x₂，y₂）．由于A、B分别在角α、β的终边上，可得sinα=y₁，cosα=x₁，sinβ=y₂，cosβ=x₂．联立

y=2x+b x2+y2=1

，得到根与系数的关系，又sin（α+β）=sinαcosβ+cosαsinβ=y₁x₂+y₂x₁=（2x₁+b）x₂+（2x₂+b）x₁=4x₁x₂+b（x₁+x₂），代入即可．

解答：解：如图所示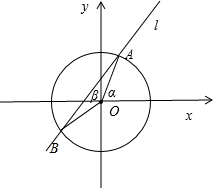，设A（x₁，y₁），B（x₂，y₂）．
∵A、B分别在角α、β的终边上，∴sinα=y₁，cosα=x₁，sinβ=y₂，cosβ=x₂．
联立

y=2x+b x2+y2=1

，5x²4bx+b²-1=0．
∴x1+x2=-

4b

5

，x1x2=

b2-1

5

．
∴sin（α+β）=sinαcosβ+cosαsinβ
=y₁x₂+y₂x₁=（2x₁+b）x₂+（2x₂+b）x₁=4x₁x₂+b（x₁+x₂）=

4(b2-1)

5

-

4b2

5

=-

4

5

．
故答案为-

4

5

．

点评：熟练掌握两角和的正弦公式、三角函数的定义、直线与圆相交问题转化为方程联立得到根与系数等是解题的关键．