题目内容
已知△ABC的内角A、B、C的对边分别为a、b、c,若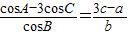 .
.(Ⅰ) 求
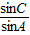 的值;
的值;(Ⅱ) 若b=2,且
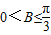 ,求边长a的取值范围.
,求边长a的取值范围.
【答案】分析:(1)把已知利用正弦定理进行化简,然后结合和差角公式及三角形的内角和定理化简即可求解
(2)由(1)sinC与sinA的关系可得c与a的关系,然后结合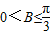 ,求cosB范围,由余弦定理b2=a2+c2-2accosB,可求
,求cosB范围,由余弦定理b2=a2+c2-2accosB,可求
解答:解:(1)由正弦定理得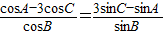 …(2分)
…(2分)
即(cosA-3cosC)sinB=(3sinC-sinA)cosB
化简可得sin(A+B)=3sin(B+C)…(4分)
又A+B+C=π,所以sinC=3sinA
因此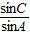 =3 …(6分)
=3 …(6分)
(2)由(1)得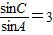 ,可得c=3a①…(8分)
,可得c=3a①…(8分)
∵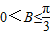 ,即
,即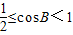 ②…(10分)
②…(10分)
由余弦定理得b2=a2+c2-2accosB,把①代入可得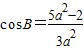 …(12分)
…(12分)
代入②式,解得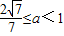 …(14分)
…(14分)
点评:本题主要考查了三角形的正弦定理、余弦定理及和差角公式的综合应用,解题的关键是熟练应用基本公式
(2)由(1)sinC与sinA的关系可得c与a的关系,然后结合
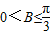 ,求cosB范围,由余弦定理b2=a2+c2-2accosB,可求
,求cosB范围,由余弦定理b2=a2+c2-2accosB,可求解答:解:(1)由正弦定理得
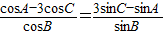 …(2分)
…(2分)即(cosA-3cosC)sinB=(3sinC-sinA)cosB
化简可得sin(A+B)=3sin(B+C)…(4分)
又A+B+C=π,所以sinC=3sinA
因此
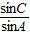 =3 …(6分)
=3 …(6分)(2)由(1)得
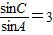 ,可得c=3a①…(8分)
,可得c=3a①…(8分)∵
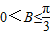 ,即
,即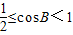 ②…(10分)
②…(10分)由余弦定理得b2=a2+c2-2accosB,把①代入可得
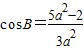 …(12分)
…(12分)代入②式,解得
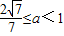 …(14分)
…(14分)点评:本题主要考查了三角形的正弦定理、余弦定理及和差角公式的综合应用,解题的关键是熟练应用基本公式

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目