题目内容
(本题满分13分)
已知函数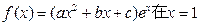 处取得极小值,其图象过点A(0,1),且在点A处切线的斜率为—1。
处取得极小值,其图象过点A(0,1),且在点A处切线的斜率为—1。
(1)求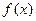 的解析式;
的解析式;
(2)设函数 上的值域也是
上的值域也是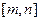 ,则称区间
,则称区间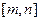 为函数
为函数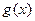 的“保值区间”。
的“保值区间”。
①证明:当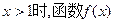 不存在“保值区间”;
不存在“保值区间”;
②函数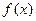 是否存在“保值区间”?若存在,写出一个“保值区间”(不必证明);若不存在,说明理由。
是否存在“保值区间”?若存在,写出一个“保值区间”(不必证明);若不存在,说明理由。
已知函数
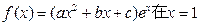 处取得极小值,其图象过点A(0,1),且在点A处切线的斜率为—1。
处取得极小值,其图象过点A(0,1),且在点A处切线的斜率为—1。(1)求
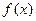 的解析式;
的解析式;(2)设函数
 上的值域也是
上的值域也是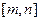 ,则称区间
,则称区间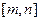 为函数
为函数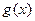 的“保值区间”。
的“保值区间”。①证明:当
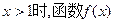 不存在“保值区间”;
不存在“保值区间”;②函数
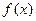 是否存在“保值区间”?若存在,写出一个“保值区间”(不必证明);若不存在,说明理由。
是否存在“保值区间”?若存在,写出一个“保值区间”(不必证明);若不存在,说明理由。
[0,1]为它的一个“保值区间”。
.解:(1)
 , ………………2分
, ………………2分
由
所以 ………………4分
………………4分
(2)由(1)得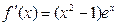 ,
,
①假设当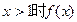 存在“保值区间”
存在“保值区间”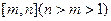
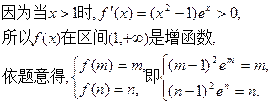
于是问题转化为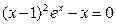 有两个大于1的不等实根。…………6分
有两个大于1的不等实根。…………6分
法一:现在考察函数 ,
,


 …………10分
…………10分
当x变化时,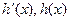 的变化情况如下表:
的变化情况如下表:
所以,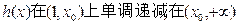 上单调递增。
上单调递增。
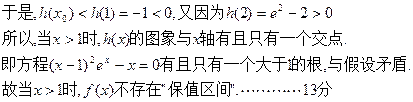
法二:于是问题转化为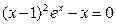 有两个大于1的不等实根。
有两个大于1的不等实根。

所以函数 的图象有且只有一个交点。
的图象有且只有一个交点。
即方程 有且只有一个大于1的实根,与假设矛盾。
有且只有一个大于1的实根,与假设矛盾。
故当 不存在“保值区间”。
不存在“保值区间”。
②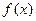 存在“保值区间”,[0,1]为它的一个“保值区间”。 ………………13分
存在“保值区间”,[0,1]为它的一个“保值区间”。 ………………13分

 , ………………2分
, ………………2分由

所以
 ………………4分
………………4分(2)由(1)得
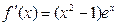 ,
,①假设当
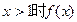 存在“保值区间”
存在“保值区间”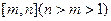
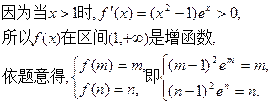
于是问题转化为
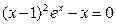 有两个大于1的不等实根。…………6分
有两个大于1的不等实根。…………6分法一:现在考察函数
 ,
,

 …………10分
…………10分当x变化时,
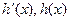 的变化情况如下表:
的变化情况如下表: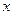 |  |  | 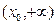 |
 | — | 0 | + |
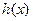 | 单调递减 | 极小值 | 单调递增 |
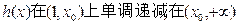 上单调递增。
上单调递增。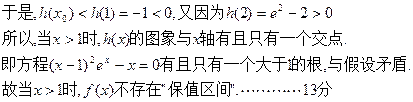
法二:于是问题转化为
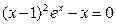 有两个大于1的不等实根。
有两个大于1的不等实根。
所以函数
 的图象有且只有一个交点。
的图象有且只有一个交点。即方程
 有且只有一个大于1的实根,与假设矛盾。
有且只有一个大于1的实根,与假设矛盾。故当
 不存在“保值区间”。
不存在“保值区间”。②
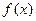 存在“保值区间”,[0,1]为它的一个“保值区间”。 ………………13分
存在“保值区间”,[0,1]为它的一个“保值区间”。 ………………13分
练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
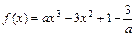 .
.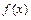 的单调性;
的单调性;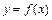 上两点A、B处的切线都与y轴垂直,且线段AB与x轴有公共点,求实数a的取值范围.
上两点A、B处的切线都与y轴垂直,且线段AB与x轴有公共点,求实数a的取值范围.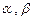 是函数
是函数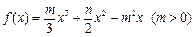 的两个极值点,且
的两个极值点,且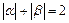 .
. 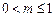 ;
; 的取值范围;
的取值范围;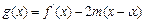 ,当
,当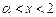 且
且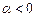 时,求证:
时,求证: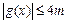 .
.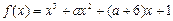 有极大值和极小值,则
有极大值和极小值,则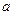 的取值范围是 .
的取值范围是 . 在
在 处取得极值,则
处取得极值,则 。
。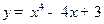 在区间[-2,3 ]上的最小值为 ( )
在区间[-2,3 ]上的最小值为 ( )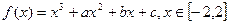 表示过原点的曲线,且在
表示过原点的曲线,且在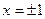 处的切线的倾斜角均为
处的切线的倾斜角均为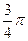 ,有以下命题:
,有以下命题: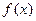 的解析式为
的解析式为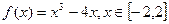 ;
;