题目内容
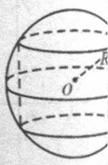
 如图,半径为R的球O中有一内接圆柱.当圆柱的侧面积最大时,球的表面积与该圆柱的侧面积之差是
如图,半径为R的球O中有一内接圆柱.当圆柱的侧面积最大时,球的表面积与该圆柱的侧面积之差是分析:设出圆柱的上底面半径为r,球的半径与上底面夹角为α,求出圆柱的侧面积表达式,求出最大值,计算球的表面积,即可得到两者的差值.
解答:解:设圆柱的上底面半径为r,球的半径与上底面夹角为α,则r=Rcosα,圆柱的高为2Rsinα,圆柱的侧面积为:2πR2sin2α,当且仅当α=
时,sin2α=1,圆柱的侧面积最大,圆柱的侧面积为:2πR2,球的表面积为:4πR2,球的表面积与该圆柱的侧面积之差是:2πR2.
故答案为:2πR2
| π |
| 4 |
故答案为:2πR2
点评:本题是基础题,考查球的内接圆柱的知识,球的表面积,圆柱的侧面积的最大值的求法,考查计算能力,常考题型.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
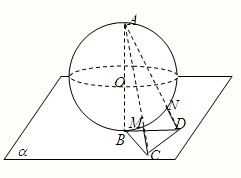 如图,半径为R的球O的直径AB垂直于平面α,垂足为B,△BCD是平面α内边长为R的正三角形,线段AC、AD分别与球面交于点M、N,那么M、N两点间的球面距离是
如图,半径为R的球O的直径AB垂直于平面α,垂足为B,△BCD是平面α内边长为R的正三角形,线段AC、AD分别与球面交于点M、N,那么M、N两点间的球面距离是