题目内容
(本题满分14分)已知等差数列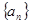 的前
的前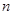 项和为
项和为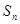 ,等比数列
,等比数列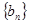 的前
的前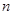 项和为
项和为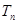 ,它们满足
,它们满足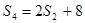 ,
,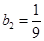 ,
,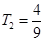 ,且当
,且当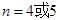 时,
时,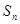 取得最小值.
取得最小值.
(Ⅰ)求数列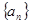 、
、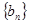 的通项公式;
的通项公式;
(Ⅱ)令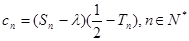 ,如果
,如果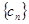 是单调数列,求实数
是单调数列,求实数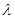 的取值范围.
的取值范围.
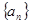 的前
的前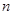 项和为
项和为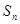 ,等比数列
,等比数列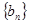 的前
的前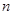 项和为
项和为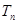 ,它们满足
,它们满足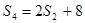 ,
,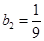 ,
,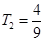 ,且当
,且当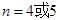 时,
时,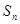 取得最小值.
取得最小值.(Ⅰ)求数列
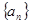 、
、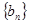 的通项公式;
的通项公式;(Ⅱ)令
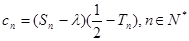 ,如果
,如果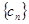 是单调数列,求实数
是单调数列,求实数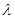 的取值范围.
的取值范围.(Ⅰ)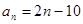 ,
, 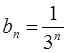 ;(Ⅱ)
;(Ⅱ)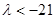
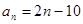 ,
, 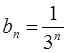 ;(Ⅱ)
;(Ⅱ)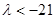
本试题主要是考查了等差数列和等比数列的定义,以及通项公式的运用,以及求和的综合运用。
(1)由于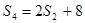 并且当
并且当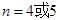 时,
时,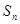 取得最小值.那么可以解得数列的通项公式。
取得最小值.那么可以解得数列的通项公式。
以及等比数列中两项的关系式,化简得到其通项公式。
(2)由上可知 ,
,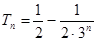 ,
, ,那么利用数列的单调性的判定可知,
,那么利用数列的单调性的判定可知,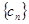 是单调数列,实数
是单调数列,实数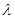 的取值范围
的取值范围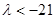
解:(Ⅰ)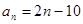 …………………4分
…………………4分
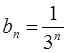 …………………6分
…………………6分
(Ⅱ) ,
,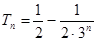 ,
, …………………9分
…………………9分
当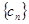 递增时,
递增时,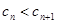 ,即
,即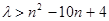 恒成立,
恒成立,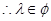 ………………11分
………………11分
当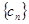 递减时,
递减时,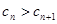 ,即
,即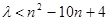 恒成立,
恒成立,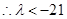
故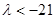 ………………14分
………………14分
(1)由于
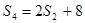 并且当
并且当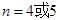 时,
时,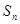 取得最小值.那么可以解得数列的通项公式。
取得最小值.那么可以解得数列的通项公式。以及等比数列中两项的关系式,化简得到其通项公式。
(2)由上可知
 ,
,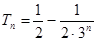 ,
, ,那么利用数列的单调性的判定可知,
,那么利用数列的单调性的判定可知,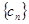 是单调数列,实数
是单调数列,实数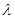 的取值范围
的取值范围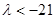
解:(Ⅰ)
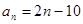 …………………4分
…………………4分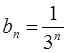 …………………6分
…………………6分(Ⅱ)
 ,
,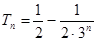 ,
, …………………9分
…………………9分当
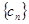 递增时,
递增时,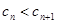 ,即
,即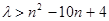 恒成立,
恒成立,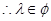 ………………11分
………………11分当
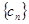 递减时,
递减时,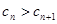 ,即
,即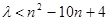 恒成立,
恒成立,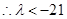
故
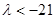 ………………14分
………………14分
练习册系列答案
相关题目
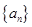 是公差为
是公差为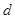 的等差数列,
的等差数列,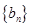 是公比为
是公比为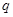 的等比数列.
的等比数列.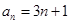 ,是否存在
,是否存在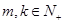 ,有
,有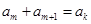 ?请说明理由;
?请说明理由;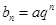 (
(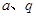 为常数,且
为常数,且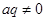 ),对任意
),对任意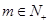 ,存在
,存在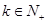 ,有
,有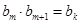 ,试求
,试求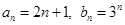 ,试确定所有的
,试确定所有的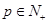 ,使数列
,使数列 项的和为数列中
项的和为数列中 ,
,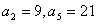
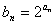 ,求数列
,求数列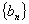 的前
的前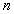 项和
项和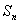 ;
;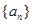 为等比数列,其前
为等比数列,其前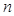 项和为
项和为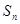 ,已知
,已知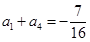 ,且对于任意的
,且对于任意的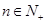 有
有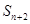 ,
,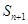 成等差;
成等差;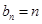 (
(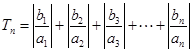 ,若
,若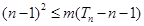 对于
对于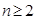 恒成立,求实数
恒成立,求实数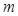 的范围.
的范围.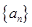 的各项均为正值,首项
的各项均为正值,首项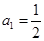 ,前n项和为
,前n项和为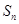 ,且
,且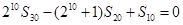
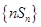 的前n项和
的前n项和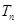
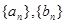 中,
中,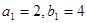 ,且
,且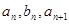 成等差数列,
成等差数列,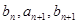 成等比数列
成等比数列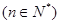 。
。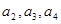 及
及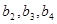 ,由此猜测
,由此猜测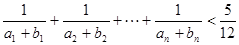 。
。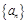 中,
中,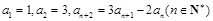 .
.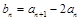 ,求证:数列
,求证:数列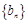 是常数列,并写出其通项公式;
是常数列,并写出其通项公式;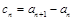 ,求证:数列
,求证:数列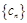 是等比数列,并写出其通项公式;
是等比数列,并写出其通项公式;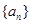 为等差数列,且
为等差数列,且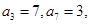 则
则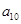 等于( )
等于( )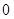
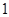
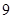
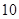
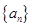 中,已知
中,已知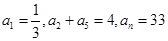 ,则
,则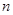 为( )
为( )