题目内容
6．某人射击8枪，命中4枪，4枪命中恰好有3枪连在一起的不同种数为20．分析 由题意，可用插空法求解，把不中的四枪看作是四个格板，格开了五个空隙，再将命中的四枪看作四个物体，由于其中有连中的三枪，此三枪绑定看作是一个物体，先插入此物体，再插入剩余的1个物体，由此计算出所有不同的情况即可选出正确答案．
解答 解：本题可用插空法解决，把不中的四枪看作是四个格板，它们排成一列，分出五个空隙，再将命中的四枪看作是插入五个空隙中的四个物体，由于其中有三枪连中，将它们绑定看作一个物体，然后分两步插入五个空隙：
第一步插入绑定三个物体，有5种方法；
第二步将剩下1个物体插入剩下的四个空隙中，有4种方法，
故总的插入方法有5×4=20（种）．
故答案为：20．
点评 本题考点是排列、组合及简单计数问题，考查插空法与绑定法，解答的关键是理解题意将问题正确转化，插空与绑定是计数中常采用的技巧，注意体会其使用的条件．
练习册系列答案
相关题目
16．某中学有甲乙两个文科班进行数学考试，按照大于或等于120分为优秀，120分以下为非优秀统计成绩后，得到如下列联表：
（Ⅰ）用分层抽样的方法在优秀的学生中抽6人，其中甲班抽多少人？
（Ⅱ）在上述抽取的6人中选2人，求恰有一名同学在乙班的概率；
（Ⅲ）计算出统计量k2，若按95%可靠性要求能否认为“成绩与班级有关”．
下面的临界值表代参考：
（参考公式k2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$其中n=a+b+c+d）
| 优秀 | 非优秀 | 合计 | |
| 甲 | 20 | 5 | 25 |
| 乙 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
（Ⅱ）在上述抽取的6人中选2人，求恰有一名同学在乙班的概率；
（Ⅲ）计算出统计量k2，若按95%可靠性要求能否认为“成绩与班级有关”．
下面的临界值表代参考：
| P（K2≥k） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
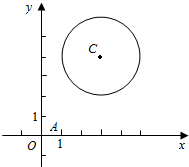已知圆C：ABCD，直线l1过定点A （1，0）．