题目内容
(理)如图,PA⊥平面ABCD,四边形ABCD是正方形,PA=AD=2,点E、F、G分别为线段PA、PD和CD的中点.(1)求异面直线EG与BD所成角的大小;
(2)在线段CD上是否存在一点Q,使得点A到平面EFQ的距离恰为
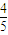 ?若存在,求出线段CQ的长;若不存在,请说明理由.
?若存在,求出线段CQ的长;若不存在,请说明理由.(文)已知坐标平面内的一组基向量为
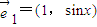 ,
,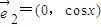 ,其中
,其中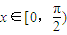 ,且向量
,且向量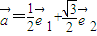 .
.(1)当
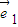 和
和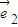 都为单位向量时,求
都为单位向量时,求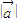 ;
;(2)若向量
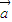 和向量
和向量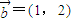 共线,求向量
共线,求向量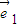 和
和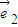 的夹角.
的夹角.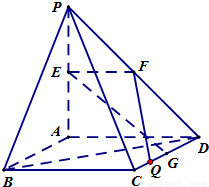
【答案】分析:(理科)(1)以点A为坐标原点,射线AB,AD,AZ分别为x轴、y轴、z轴的正半轴建系如图示,写出点E(0,0,1)、G(1,2,0)、B(2,0,0)、D(0,2,0),和向量 ,
, 的坐标,利用异面直线EG与BD所成角公式求出异面直线EG与BD所成角大小即可;
的坐标,利用异面直线EG与BD所成角公式求出异面直线EG与BD所成角大小即可;
(2)对于存在性问题,可先假设存在,即先假设在线段CD上存在一点Q满足条件,设点Q(x,2,0),平面EFQ的法向量为 ,再点A到平面EFQ的距离,求出x,若出现矛盾,则说明假设不成立,即不存在;否则存在.
,再点A到平面EFQ的距离,求出x,若出现矛盾,则说明假设不成立,即不存在;否则存在.
(文科)(1)由题意,得出 ,
, 都为单位向量.从而求得
都为单位向量.从而求得 .
.
(2)由条件 ,因为向量
,因为向量 和向量
和向量 共线,根据共线向量的性质求得:
共线,根据共线向量的性质求得: .最后利用向量
.最后利用向量 和
和 的夹角即可求得向量
的夹角即可求得向量 和
和 的夹角.
的夹角.
解答: 解:(理科)(1)以点A为坐标原点,射线AB,AD,AZ分别为x轴、y轴、z轴的正半轴建立空间直角坐标系如图示,点E(0,0,1)、G(1,2,0)、B(2,0,0)、D(0,2,0),
解:(理科)(1)以点A为坐标原点,射线AB,AD,AZ分别为x轴、y轴、z轴的正半轴建立空间直角坐标系如图示,点E(0,0,1)、G(1,2,0)、B(2,0,0)、D(0,2,0),
则 ,
, .
.
设异面直线EG与BD所成角为θ =
= ,
,
所以异面直
线EG与BD所成角大小为 .
.
(2)假设在线段CD上存在一点Q满足条件,设点Q(x,2,0),平面EFQ的法向量为 ,
,
则有 得到y=0,z=xx,取x=1,
得到y=0,z=xx,取x=1,
所以 ,则
,则 ,又x>0,解得
,又x>0,解得 ,
,
所以点 即
即 ,则
,则 .
.
所以在线段CD上存在一点Q满足条件,且长度为 .
.
(文科)解:(1)由题意,当x=0时,sinx=0,cosx=1,此时 ,
, 都为单位向量.
都为单位向量.
故 ,
,
所以 .
.
(2)由条件
因为向量 和向量
和向量 共线,
共线,
所以
 ,
,
因为 ,
,
所以 .
.
于是 ,
, ,
,
设向量 和
和 的夹角为θ
的夹角为θ
则 =
= ,
,
即向量 和
和 的夹角为
的夹角为 .
.
点评:考查利用空间向量证明垂直和求夹角和距离问题,以及平行向量与共线向量的判定定理,体现 了转化的思想方法,属中档题.
 ,
, 的坐标,利用异面直线EG与BD所成角公式求出异面直线EG与BD所成角大小即可;
的坐标,利用异面直线EG与BD所成角公式求出异面直线EG与BD所成角大小即可;(2)对于存在性问题,可先假设存在,即先假设在线段CD上存在一点Q满足条件,设点Q(x,2,0),平面EFQ的法向量为
 ,再点A到平面EFQ的距离,求出x,若出现矛盾,则说明假设不成立,即不存在;否则存在.
,再点A到平面EFQ的距离,求出x,若出现矛盾,则说明假设不成立,即不存在;否则存在.(文科)(1)由题意,得出
 ,
, 都为单位向量.从而求得
都为单位向量.从而求得 .
.(2)由条件
 ,因为向量
,因为向量 和向量
和向量 共线,根据共线向量的性质求得:
共线,根据共线向量的性质求得: .最后利用向量
.最后利用向量 和
和 的夹角即可求得向量
的夹角即可求得向量 和
和 的夹角.
的夹角.解答:
 解:(理科)(1)以点A为坐标原点,射线AB,AD,AZ分别为x轴、y轴、z轴的正半轴建立空间直角坐标系如图示,点E(0,0,1)、G(1,2,0)、B(2,0,0)、D(0,2,0),
解:(理科)(1)以点A为坐标原点,射线AB,AD,AZ分别为x轴、y轴、z轴的正半轴建立空间直角坐标系如图示,点E(0,0,1)、G(1,2,0)、B(2,0,0)、D(0,2,0),则
 ,
, .
.设异面直线EG与BD所成角为θ
 =
= ,
,所以异面直
线EG与BD所成角大小为
 .
.(2)假设在线段CD上存在一点Q满足条件,设点Q(x,2,0),平面EFQ的法向量为
 ,
,则有
 得到y=0,z=xx,取x=1,
得到y=0,z=xx,取x=1,所以
 ,则
,则 ,又x>0,解得
,又x>0,解得 ,
,所以点
 即
即 ,则
,则 .
.所以在线段CD上存在一点Q满足条件,且长度为
 .
.(文科)解:(1)由题意,当x=0时,sinx=0,cosx=1,此时
 ,
, 都为单位向量.
都为单位向量.故
 ,
,所以
 .
.(2)由条件

因为向量
 和向量
和向量 共线,
共线,所以

 ,
,因为
 ,
,所以
 .
.于是
 ,
, ,
,设向量
 和
和 的夹角为θ
的夹角为θ则
 =
= ,
,即向量
 和
和 的夹角为
的夹角为 .
.点评:考查利用空间向量证明垂直和求夹角和距离问题,以及平行向量与共线向量的判定定理,体现 了转化的思想方法,属中档题.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
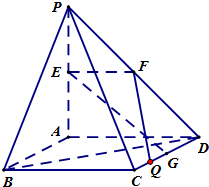 (理)如图,PA⊥平面ABCD,四边形ABCD是正方形,PA=AD=2,点E、F、G分别为线段PA、PD和CD的中点.
(理)如图,PA⊥平面ABCD,四边形ABCD是正方形,PA=AD=2,点E、F、G分别为线段PA、PD和CD的中点. (2011•崇明县二模)(理)如图,PA⊥平面ABCD,四边形ABCD是正方形,PA=AD=2,点E、F、G分别为线段PA、PD和CD的中点.
(2011•崇明县二模)(理)如图,PA⊥平面ABCD,四边形ABCD是正方形,PA=AD=2,点E、F、G分别为线段PA、PD和CD的中点.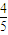 ?若存在,求出线段CQ的长;若不存在,请说明理由.
?若存在,求出线段CQ的长;若不存在,请说明理由.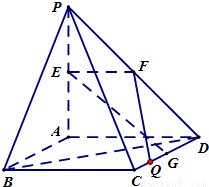
 ?若存在,求出线段CQ的长;若不存在,请说明理由.
?若存在,求出线段CQ的长;若不存在,请说明理由.