题目内容
(本小题满分14分)已知函数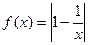 ,(x>0).
,(x>0).
(1)当0<a<b,且f(a)=f(b)时,求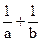 的值 ;
的值 ;
(2)是否存在实数a,b(a<b),使得函数y=f(x)的定义域、值域都是[a,b],若存在,求出a,b的值,若不存在,请说明理由.
(3) 若存在实数a,b(a<b),使得函数y=f(x)的定义域为 [a,b]时,值域为 [
若存在实数a,b(a<b),使得函数y=f(x)的定义域为 [a,b]时,值域为 [ ma,mb],(m≠0),求m的取值范围.
ma,mb],(m≠0),求m的取值范围.
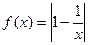 ,(x>0).
,(x>0).(1)当0<a<b,且f(a)=f(b)时,求
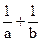 的值 ;
的值 ; (2)是否存在实数a,b(a<b),使得函数y=f(x)的定义域、值域都是[a,b],若存在,求出a,b的值,若不存在,请说明理由.
(3)
 若存在实数a,b(a<b),使得函数y=f(x)的定义域为 [a,b]时,值域为 [
若存在实数a,b(a<b),使得函数y=f(x)的定义域为 [a,b]时,值域为 [ ma,mb],(m≠0),求m的取值范围.
ma,mb],(m≠0),求m的取值范围. (14分)(1)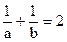 .
.
 (2)不存在满足条件的实数a,b.
(2)不存在满足条件的实数a,b.
 (3)
(3)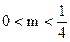
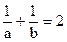 .
. (2)不存在满足条件的实数a,b.
(2)不存在满足条件的实数a,b. (3)
(3)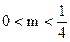
(14分)解:(1)∵x>0,∴
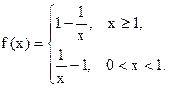
∴f(x)在(0,1)上为减函数,在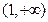 上是增函数.
上是增函数.
由0<a<b,且f(a)=f(b),可得 0<a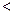 1<b和
1<b和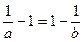 .即
.即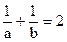 .
.
……………………3分
 (2)不存在满足条件的实数a,b.
(2)不存在满足条件的实数a,b.
若存在满足条件的实数a,b,使得函数y=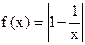 的定义域、值域都是[a,b],
的定义域、值域都是[a,b],
则a>0. 而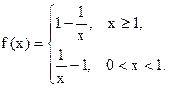
①当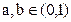 时,
时,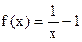 在(0,1)上为减函数.
在(0,1)上为减函数.
故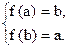 即
即 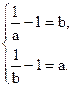 解得 a=b.
解得 a=b.
故此时不存在适合条件的实数a,b.
②当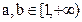 时,
时,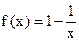 在
在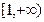 上是增函数.
上是增函数.
故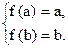 即
即 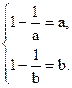
此时a,b 是方程
是方程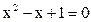 的根,此方程无实根.
的根,此方程无实根.
故此时不存在适合条件的实数a,b.
③当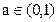 ,
,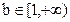 时,由于
时,由于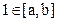 ,而
,而 ,
,
故此时不存在适合条件的实数a,b.
综上可知,不存在适合条件的实数a,b. …………………………8分
 (3)若存在实数a,b(a<b),使得函数y=f(x)的定义域为[a,b]时,值域为[ma,mb].
(3)若存在实数a,b(a<b),使得函数y=f(x)的定义域为[a,b]时,值域为[ma,mb].
则a>0,m>0.
① 当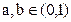 时,由于f(x)在(0,1)上是减函数,故
时,由于f(x)在(0,1)上是减函数,故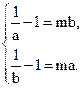 .此时得a=b,不符合题意,所以a,b不存在.
.此时得a=b,不符合题意,所以a,b不存在.
② 当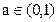 ,
,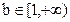 时
时 ,由(2)知0在值域内,值域不可能是[m
,由(2)知0在值域内,值域不可能是[m a,mb],所以a,b不存在.
a,mb],所以a,b不存在.
故只有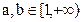 .
.
∵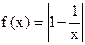 在
在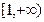
 上是增函数,
上是增函数,
∴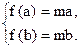 即
即 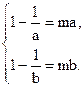 所以a、b是方程
所以a、b是方程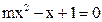 的两个根.
的两个根.
即关于x的方程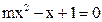 有两个大于或等于1的相异实根.
有两个大于或等于1的相异实根.
设这两个根为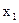 、
、 ,则
,则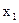 +
+ =
=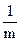 ,
,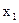 ·
· =
=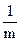 .
.
∴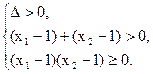 即
即 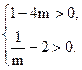 解得
解得 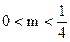 .
.
故m的取值范围是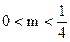 . ……………………………14分
. ……………………………14分

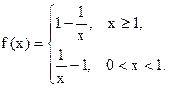
∴f(x)在(0,1)上为减函数,在
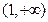 上是增函数.
上是增函数.由0<a<b,且f(a)=f(b),可得 0<a
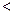 1<b和
1<b和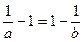 .即
.即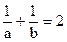 .
.……………………3分

 (2)不存在满足条件的实数a,b.
(2)不存在满足条件的实数a,b.若存在满足条件的实数a,b,使得函数y=
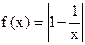 的定义域、值域都是[a,b],
的定义域、值域都是[a,b],则a>0. 而
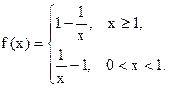
①当
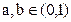 时,
时,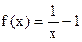 在(0,1)上为减函数.
在(0,1)上为减函数.故
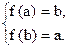 即
即 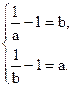 解得 a=b.
解得 a=b.故此时不存在适合条件的实数a,b.
②当
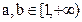 时,
时,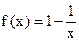 在
在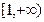 上是增函数.
上是增函数.故
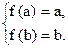 即
即 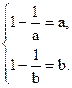
此时a,b
 是方程
是方程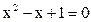 的根,此方程无实根.
的根,此方程无实根.故此时不存在适合条件的实数a,b.
③当
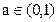 ,
,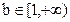 时,由于
时,由于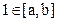 ,而
,而 ,
,故此时不存在适合条件的实数a,b.
综上可知,不存在适合条件的实数a,b. …………………………8分
 (3)若存在实数a,b(a<b),使得函数y=f(x)的定义域为[a,b]时,值域为[ma,mb].
(3)若存在实数a,b(a<b),使得函数y=f(x)的定义域为[a,b]时,值域为[ma,mb].则a>0,m>0.
① 当
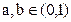 时,由于f(x)在(0,1)上是减函数,故
时,由于f(x)在(0,1)上是减函数,故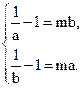 .此时得a=b,不符合题意,所以a,b不存在.
.此时得a=b,不符合题意,所以a,b不存在. ② 当
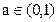 ,
,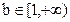 时
时 ,由(2)知0在值域内,值域不可能是[m
,由(2)知0在值域内,值域不可能是[m a,mb],所以a,b不存在.
a,mb],所以a,b不存在.故只有
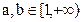 .
. ∵
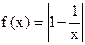 在
在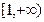
 上是增函数,
上是增函数,∴
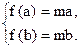 即
即 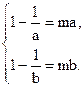 所以a、b是方程
所以a、b是方程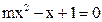 的两个根.
的两个根.即关于x的方程
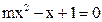 有两个大于或等于1的相异实根.
有两个大于或等于1的相异实根.设这两个根为
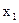 、
、 ,则
,则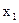 +
+ =
=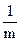 ,
,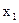 ·
· =
=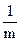 .
.∴
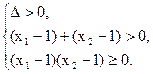 即
即 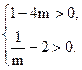 解得
解得 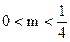 .
.故m的取值范围是
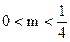 . ……………………………14分
. ……………………………14分
练习册系列答案
相关题目
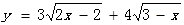 最大值为 ( )
最大值为 ( )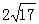
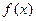 在区间
在区间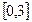 上的图象如图所示,即
上的图象如图所示,即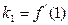 ,
,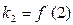 ,
,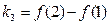 ,则
,则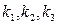 之间的大小关系为( )
之间的大小关系为( )




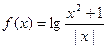
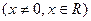 有如下命题:
有如下命题: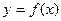 图像关于
图像关于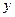 轴对称;
轴对称;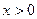 时,
时,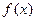 是增函数,
是增函数, 时,
时,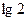 ;
;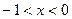 或
或 时,
时, 的单调递减区间是__________.
的单调递减区间是__________.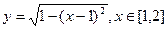 对于满足
对于满足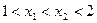 的任意
的任意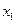 ,
,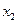 ,给出下列结论:
,给出下列结论: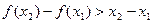 ; ②
; ②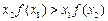 ;
;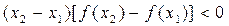 . ④
. ④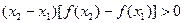
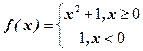 ,则满足不等式
,则满足不等式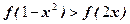 的x的范围是____ ____
的x的范围是____ ____ 加4万元,每年销售环保建材的收入为50万元. 则该厂获取的纯利润达到最大值时是在第 年.
加4万元,每年销售环保建材的收入为50万元. 则该厂获取的纯利润达到最大值时是在第 年.